
Der Frequenzgang ist der Zusammenhang zwischen Ein- und Ausgangssignal eines linearen zeitinvarianten Systems (LZI-System) bei einer sinusförmigen Anregung bezüglich der Amplitude und der Phase. Er ist daher eine komplexe Funktion der Frequenz.
Das Ausgangssignal hat wegen des linearen Verhaltens des Systems dieselbe Frequenz wie das Eingangssignal. Die beiden Signale unterscheiden sich jedoch in der Amplitude und in der Phase. Das Verhältnis der Amplituden von Eingangssignal und Ausgangssignal in Abhängigkeit von der Frequenz ist der Amplitudengang, bisweilen auch Betragsfrequenzgang genannt. Der Unterschied der Phase zwischen Eingangssignal und Ausgangssignal in Abhängigkeit von der Frequenz ist der Phasengang.
Der Frequenzgang kann auch aus der Fourier-Transformierten der Impulsantwort des Systems bestimmt werden.[1]
Der Frequenzgang beschreibt den Zusammenhang zwischen sinusförmigen Schwingungen am Ein- und Ausgang eines Systems (Übertragungsgliedes) als Funktion der Frequenz f oder der Kreisfrequenz ω.
Das System hat dabei folgende Eigenschaften:
پاسخ فركانسي چيست
Ein solches System hat bei harmonischem Eingangssignal
ein harmonisches Ausgangssignal:
Auf Grund der Linearität wird die Kreisfrequenz ω{displaystyle omega ;} nicht beeinflusst. Lediglich Amplitude (x^{displaystyle {hat {x}};} → y^{displaystyle {hat {y}};}) und Phase (ϕx{displaystyle phi _{x};} → ϕy{displaystyle phi _{y};}) werden verändert.
Der Amplituden-Frequenzgang ist das Verhältnis
Der Phasen-Frequenzgang ist die Phasendifferenz
Zur anschaulichen Darstellung des Frequenzgangs dient das Bode-Diagramm (siehe Abbildung). In je einem Graph ist der Amplituden-Frequenzgang und der Phasen-Frequenzgang dargestellt. Die Achsen sind mehrheitlich logarithmisch geteilt (außer der für die Phasenverschiebung), was den Gebrauch des Diagramms erleichtert. So ist zum Beispiel die Multiplikation zweier Frequenzgänge eine einfache Streckenaddition, und die Inversion eines Frequenzgangs ergibt sich durch Spiegelung an der f- oder ω- Achse im Diagramm.[2]
Eine alternative anschauliche Darstellung des Frequenzgangs ist seine Ortskurve. Dieses Zeigerbild enthält im Gegensatz zum Bode-Diagramm beide Informationen: Die Zeigerlänge entspricht dem Amplitudenverhältnis, sein Argument φ ist die Phasenverschiebung.
Diese Ortskurve wird auch Nyquist-Diagramm genannt. Mit der Vorstellung, dass in der (komplexen) Ebene lediglich die Spitzen eingefrorener Zeiger zur Ortskurve verbunden sind, kann der Frequenzgang ohne Kenntnis der komplexen Mathematik und der mathematischen Transformationen aus dem Zeit- in den Frequenzbereich anschaulich gemacht werden.
LZI-Systeme mit endlich vielen inneren Freiheitsgraden werden durch die lineare Differentialgleichung n-ter Ordnung im Zeitbereich (Zeit als Variable) beschrieben:
Die Anwendung der Fourier-Transformation auf die Differentialgleichung führt zum Frequenzgang als Bild-Funktion in der komplexen Zahlenebene.
Frequenzgang H(jω){displaystyle H(mathrm {j} omega )} ist der Quotient aus den Fouriertransformierten Y(jω){displaystyle Y(mathrm {j} omega )} des Ausgangs-Signals und X(jω){displaystyle X(mathrm {j} omega )} des Eingangs-Signals:
Fourier-Rücktransformierte des Frequenzganges ist die Gewichtsfunktion oder Impulsantwort:
Schreibweisen des Frequenzgangs:
siehe Hauptartikel: Übertragungsfunktion
Mit σ=0{displaystyle sigma =0} in s=σ+jω{displaystyle s=sigma +jomega } geht die Laplace-Übertragungsfunktion F(s){displaystyle F(s)} in den Frequenzgang F(ω){displaystyle F(omega )} über.
Der Frequenzgang beschreibt daher keine Übergangsvorgänge (Einschwingvorgänge durch Zeitkonstanten). Und er ist auch nicht geeignet zur Beschreibung von instabilen aufklingenden Systemen.
Die Laplace-Übertragungsfunktion ist in diesen Aspekten durch den zusätzlichen Parameter σ{displaystyle sigma } allgemeiner.
Die Bedeutung des Frequenzgangs für LZI-Systeme beruht auf der Einfachheit seiner experimentellen Gewinnung. Dazu wird das System mit einem Signalgenerator mit verschiedenen Frequenzen angeregt und die Systemantwort gemessen.
Bei Systemen mit einem schnellen Einschwingverhalten nach einer (kleinen) Frequenzänderung kann die Messung mittels eines Wobbelgenerators erfolgen, wie zum Beispiel in der Nachrichtentechnik. Der Wobbelgenerator ist ein spezieller Signalgenerator, der seine Ausgangs-Frequenz kontinuierlich ändert.
Falls jedoch nach jeder Frequenzanregung zunächst eine gewisse Zeit abgewartet werden muss, bis sich die Amplitude der Systemantwort nicht mehr ändert, dann ist der Prozess mit Hilfe eines Signalgenerators zeitaufwändiger.[3]
In diesem Fall ist es einfacher das System mit allen interessierenden Frequenzen gleichzeitig anzuregen und den Frequenzgang beispielsweise über die Messung der Impulsantwort zu bestimmen.
In jedem Fall benötigt die experimentelle Frequenzgang-Bestimmung eine zeitsynchrone Messung des Eingangssignals x und des Ausgangssignal y des Systems.
In einem allgemeineren Sinn kann mit „Frequenzgang“ auch eine andere frequenzabhängige Eigenschaft eines physikalischen Systems gemeint sein, wie zum Beispiel die Leistungsaufnahme, die Temperatur oder die Strahlungsleistung als Funktion der Frequenz.[4][5] Gebräuchlicher als z. B. „Frequenzgang einer Leistung“ ist allerdings die Ausdrucksweise „Frequenzabhängigkeit einer Leistung“. Einer Quelle zufolge bezeichnet „Frequenzgang“ im Sprachgebrauch der Regelungstechniker auch das bekannte Frequenzspektrum von speziellen nichtperiodischen Anregungssignalen.[6]
Kennen Sie den Frequenzgang des Gehörs?![]()
Der Frequenzgang ist der Zusammenhang zwischen Ein- und Ausgangssignal eines linearen zeitinvarianten Systems (LZI-System) bei einer sinusförmigen Anregung bezüglich der Amplitude und der Phase. Er ist daher eine komplexe Funktion der Frequenz.
Das Ausgangssignal hat wegen des linearen Verhaltens des Systems dieselbe Frequenz wie das Eingangssignal. Die beiden Signale unterscheiden sich jedoch in der Amplitude und in der Phase. Das Verhältnis der Amplituden von Eingangssignal und Ausgangssignal in Abhängigkeit von der Frequenz ist der Amplitudengang, bisweilen auch Betragsfrequenzgang genannt. Der Unterschied der Phase zwischen Eingangssignal und Ausgangssignal in Abhängigkeit von der Frequenz ist der Phasengang.
Der Frequenzgang kann auch aus der Fourier-Transformierten der Impulsantwort des Systems bestimmt werden.[1]
Der Frequenzgang beschreibt den Zusammenhang zwischen sinusförmigen Schwingungen am Ein- und Ausgang eines Systems (Übertragungsgliedes) als Funktion der Frequenz f oder der Kreisfrequenz ω.
Das System hat dabei folgende Eigenschaften:
پاسخ فركانسي چيست
Ein solches System hat bei harmonischem Eingangssignal
ein harmonisches Ausgangssignal:
Auf Grund der Linearität wird die Kreisfrequenz ω{displaystyle omega ;} nicht beeinflusst. Lediglich Amplitude (x^{displaystyle {hat {x}};} → y^{displaystyle {hat {y}};}) und Phase (ϕx{displaystyle phi _{x};} → ϕy{displaystyle phi _{y};}) werden verändert.
Der Amplituden-Frequenzgang ist das Verhältnis
Der Phasen-Frequenzgang ist die Phasendifferenz
Zur anschaulichen Darstellung des Frequenzgangs dient das Bode-Diagramm (siehe Abbildung). In je einem Graph ist der Amplituden-Frequenzgang und der Phasen-Frequenzgang dargestellt. Die Achsen sind mehrheitlich logarithmisch geteilt (außer der für die Phasenverschiebung), was den Gebrauch des Diagramms erleichtert. So ist zum Beispiel die Multiplikation zweier Frequenzgänge eine einfache Streckenaddition, und die Inversion eines Frequenzgangs ergibt sich durch Spiegelung an der f- oder ω- Achse im Diagramm.[2]
Eine alternative anschauliche Darstellung des Frequenzgangs ist seine Ortskurve. Dieses Zeigerbild enthält im Gegensatz zum Bode-Diagramm beide Informationen: Die Zeigerlänge entspricht dem Amplitudenverhältnis, sein Argument φ ist die Phasenverschiebung.
Diese Ortskurve wird auch Nyquist-Diagramm genannt. Mit der Vorstellung, dass in der (komplexen) Ebene lediglich die Spitzen eingefrorener Zeiger zur Ortskurve verbunden sind, kann der Frequenzgang ohne Kenntnis der komplexen Mathematik und der mathematischen Transformationen aus dem Zeit- in den Frequenzbereich anschaulich gemacht werden.
LZI-Systeme mit endlich vielen inneren Freiheitsgraden werden durch die lineare Differentialgleichung n-ter Ordnung im Zeitbereich (Zeit als Variable) beschrieben:
Die Anwendung der Fourier-Transformation auf die Differentialgleichung führt zum Frequenzgang als Bild-Funktion in der komplexen Zahlenebene.
Frequenzgang H(jω){displaystyle H(mathrm {j} omega )} ist der Quotient aus den Fouriertransformierten Y(jω){displaystyle Y(mathrm {j} omega )} des Ausgangs-Signals und X(jω){displaystyle X(mathrm {j} omega )} des Eingangs-Signals:
Fourier-Rücktransformierte des Frequenzganges ist die Gewichtsfunktion oder Impulsantwort:
Schreibweisen des Frequenzgangs:
siehe Hauptartikel: Übertragungsfunktion
Mit σ=0{displaystyle sigma =0} in s=σ+jω{displaystyle s=sigma +jomega } geht die Laplace-Übertragungsfunktion F(s){displaystyle F(s)} in den Frequenzgang F(ω){displaystyle F(omega )} über.
Der Frequenzgang beschreibt daher keine Übergangsvorgänge (Einschwingvorgänge durch Zeitkonstanten). Und er ist auch nicht geeignet zur Beschreibung von instabilen aufklingenden Systemen.
Die Laplace-Übertragungsfunktion ist in diesen Aspekten durch den zusätzlichen Parameter σ{displaystyle sigma } allgemeiner.
Die Bedeutung des Frequenzgangs für LZI-Systeme beruht auf der Einfachheit seiner experimentellen Gewinnung. Dazu wird das System mit einem Signalgenerator mit verschiedenen Frequenzen angeregt und die Systemantwort gemessen.
Bei Systemen mit einem schnellen Einschwingverhalten nach einer (kleinen) Frequenzänderung kann die Messung mittels eines Wobbelgenerators erfolgen, wie zum Beispiel in der Nachrichtentechnik. Der Wobbelgenerator ist ein spezieller Signalgenerator, der seine Ausgangs-Frequenz kontinuierlich ändert.
Falls jedoch nach jeder Frequenzanregung zunächst eine gewisse Zeit abgewartet werden muss, bis sich die Amplitude der Systemantwort nicht mehr ändert, dann ist der Prozess mit Hilfe eines Signalgenerators zeitaufwändiger.[3]
In diesem Fall ist es einfacher das System mit allen interessierenden Frequenzen gleichzeitig anzuregen und den Frequenzgang beispielsweise über die Messung der Impulsantwort zu bestimmen.
In jedem Fall benötigt die experimentelle Frequenzgang-Bestimmung eine zeitsynchrone Messung des Eingangssignals x und des Ausgangssignal y des Systems.
In einem allgemeineren Sinn kann mit „Frequenzgang“ auch eine andere frequenzabhängige Eigenschaft eines physikalischen Systems gemeint sein, wie zum Beispiel die Leistungsaufnahme, die Temperatur oder die Strahlungsleistung als Funktion der Frequenz.[4][5] Gebräuchlicher als z. B. „Frequenzgang einer Leistung“ ist allerdings die Ausdrucksweise „Frequenzabhängigkeit einer Leistung“. Einer Quelle zufolge bezeichnet „Frequenzgang“ im Sprachgebrauch der Regelungstechniker auch das bekannte Frequenzspektrum von speziellen nichtperiodischen Anregungssignalen.[6]
Kennen Sie den Frequenzgang des Gehörs?![]()
پاسخ فرکانسی یک سیستم عبارت است از پاسخ آن به تحریکهای اِعمالشده در فرکانسهای مختلف، پس از چشمپوشی از پاسخ گذرای سیستم.
از نظر ریاضی، پاسخ فرکانسی سیستم برابر است با نسبت طیف فرکانسی خروجی (پاسخ) سیستم به طیف فرکانسی ورودی (تحریک) آن. از دیدگاهی دیگر، پاسخ فرکانسی سیستم، تبدیل فوریهٔ پاسخ ضربهٔ آن است.
پاسخ فرکانسی سیستم، در حالت کلی، تابعی مختلط است که دامنه (قدر مطلق) و فاز آن با فرکانس تغییر میکند.
در سادهترین تعریف، اگر یک تحریک (ورودی) سینوسی با دامنه، فرکانس و فازی معیّن به یک سیستم خطی اِعمال شود، این سیستم در همان فرکانس پاسخ خواهد داد، بهطوریکه دامنه و فاز پاسخ (خروجی) سیستم به این تحریک، بر اساس پاسخ فرکانسی سیستم، قابل تعیین خواهد بود. اگر سیستم تغییرناپذیر با زمان باشد، پاسخ فرکانسی نیز با زمان تغییر نخواهد کرد.
چهبسا هدف سیستمهای صوتی، بازتولید سیگنال ورودی بدون بروز هرگونه اعوجاج هارمونیکی در آن باشد. به این منظور، پاسخ فرکانسی یک سیستم صوتی ایدهآل میبایست دارای دامنۀ (قدر مطلق پاسخ فرکانسی) ثابتی در محدودۀ فرکانسهای صوتی (حدود 20 هرتز تا 20 کیلوهرتز) باشد. از سوی دیگر، فاز پاسخ فرکانسی سیستم در این محدوده هم میبایست به طور خطی با فرکانس تغییر کند تا همۀ فرکانسهای سیگنال صوتی به یک میزان دچار تأخیر شوند.
پاسخ فركانسي چيست
مشارکتکنندگان ویکیپدیا. «Frequency response». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۳ دسامبر ۲۰۰۸.
منبع:ویکیپدیا به زبان انگلیسی
همانگونه که از نام تقویتکنندهها و فیلترها بر میآید، با هدف تقویتکنندگی و فیلترسازی در بسیاری از مدارهای الکترونیکی به کار میروند.
تقویتکنندهها، با بهره مشخص، سیگنال را تقویت میکنند، در حالی که فیلترها، مشخصه دامنه و یا فاز یک سیگنال الکتریکی را نسبت به فرکانس آن، تغییر میدهند. از آنجایی که فیلترها و تقویتکنندهها، از مقاومت، سلف یا خازن در مدار خود استفاده میکنند، رابطه مهمی بین استفاده از این عناصر غیرفعال و مشخصه پاسخ فرکانسی مدار وجود دارد.
وقتی با مدارهای AC سر و کار داریم، فرض میکنیم در یک فرکانس ثابت (مثلاً 50 یا 60 هرتز) کار میکنند. اما پاسخ یک مدار AC خطی را میتوان با یک سیگنال ورودی AC یا سینوسی با دامنه ثابت و فرکانس متغیر آزمایش کرد. بنابراین، پاسخ فرکانسی، ابزار مناسبی برای تحلیل مدارها است.
با کمک پاسخ فرکانسی یک مدار الکتریکی یا الکترونیکی، میتوان دقیقاً فهمید که بهره (یا پاسخ دامنه) و فاز (یا پاسخ فاز) خروجی در یک فرکانس مشخص یا در محدودهای از فرکانسهای مختلف، چگونه تغییر میکنند.
معمولاً تحلیل پاسخ فرکانسی یک مدار یا سیستم، با رسم بهره آن انجام میشود که همان اندازه خروجی نسبت به ورودی است. با دانستن مقدار بهره (یا تلفات) مدار در هر فرکانس، میتوان فهمید که مدار چگونه به سیگنالهایی با فرکانسهای مختلف پاسخ میدهد و چه تاثیری روی آنها دارد.پاسخ فركانسي چيست
پاسخ فرکانسی یک مدارِ وابسته به فرکانس را میتوان در قالب شکل گرافیکی دامنه (بهره) بر حسب فرکانس ($$f$$) رسم کرد. محور افقی فرکانس، معمولاً با مقیاس لگاریتمی تعیین میشود، در حالی که محور عمودی معمولاً مقیاس خطی دارد و معرف خروجی یا بهره ولتاژ است. از آنجایی که بهره سیستم ممکن است مثبت یا منفی باشد، محور y شامل مقادیر مثبت و منفی است.
در الکترونیک، لگاریتم یا به اختصار log، توان مربوط به عدد پایه است که باید به آن اعمال شود و عدد مورد نظر (که لگاریتم آن گرفته میشود) را ارائه دهد. در یک «نمودار بود» (Bode plot)، محور x با اندازههای $$log_{10}$$ درجهبندی میشود، بنابراین هر «دهه» (Decade) فرکانس (برای مثال 0.01، 0.1، 1، 10، 100، 1000 و غیره) با فواصل یکسان روی محور مشخص خواهد شد. عمل مخالف لگاریتم، «آنتی لگاریتم» یا antilog است.
نمایش گرافیکی منحنیهای پاسخ فرکانسی، «نمودارهای بود» (Bode Plots) نامیده میشوند و از آنجایی که در آنها، محور x لگاریتمی و محور y خطی است، به این نمودارها، شیبهلگاریتمی یا نیمه لگاریتمی نیز میگویند.
پاسخ فرکانسی هر مدار، تغییرات رفتار آن نسبت به تغییرات فرکانس سیگنال ورودی است. محدوده فرکانسها چه بزرگ و چه کوچک، بین $$f_L$$ و $$f_H$$ قرار دارد که «پهنای باند» نامیده میشود. بنابراین، میتوانیم بهره ولتاژ (برحسب dB) را برای هر ورودی سینوسی در محدوده فرکانسی تعیین کنیم.
گفتیم که نمودار بود، یک نمایش لگاریتمی از پاسخ فرکانسی است. همانطور که در شکل بالا نشان داده شده است، اکثر تقویتکنندههای صوتی مدرن، یک پاسخ فرکانسی تخت در محدوده فرکانسهای صوتی 20Hz تا 20kHz دارند. این محدوده فرکانسی برای یک تقویتکننده صوتی، «پهنای باند» (Bandwidth) یا BW آن نامیده شده و از روی پاسخ فرکانسی تعیین میشود.
نقاط $$f_L$$ و $$f_H$$ متناظر با فرکانس گوشه یا قطع پایین و فرکانس گوشه یا قطع بالا، به ترتیب، نقاط افت بهره در فرکانسهای پایین و بالا هستند. این نقاط روی منحنی پاسخ فرکانسی به عنوان نقاط 3dB- شناخته میشوند. بنابراین، پهنای باند را میتوان به سادگی به صورت زیر محاسبه کرد:
دسیبل (dB) که یکدهم بل (B) است، یک واحد غیرخطی رایج برای اندازهگیری بهره است و به صورت $$20log_{10}(A)$$ تعریف میشود که در آن، A بهره دسیمال است و محور y آن را نشان میدهد. صفر دسیبل (0dB)، بیانگر عدد ۱ است که حداکثر خروجی را مشخص میکند. به عبارت دیگر، 0dB وقتی رخ میدهد که Vout=Vin باشد و میرایی یا تضعیف در این فرکانس وجود نداشته باشد.
در نمودار بود بالا میتوان دو نقطه فرکانس گوشه یا قطع مشاهده کرد که در آن، خروجی از 0dB به 3dB- افت میکند و به یک مقدار ثابت میرسد. این افت یا کاهش بهره، معمولاً با نام «افت آرام» (roll-off rate) شناخته شده و به اندازه 20dB/decade تعریف میشود و معادل 6dB/octave است. این مقادیر با توجه به مرتبه مدار، چند برابر میشوند.
نقاط فرکانس گوشه ۳dB- فرکانسهایی هستند که در آنها بهره خروجی تا ۷0.71 درصد مقدار ماکزیمم کاهش مییابد. بنابراین، میتوان گفت نقطه ۳dB- فرکانسی است که بهره سیستم به 0.707 مقدار حداکثرش میرسد.
نقطه 3dB- به عنوان نقاط نصف توان نیز شناخته میشود، زیرا توان خروجی در این فرکانسهای گوشه، نصف حداکثر آن در 0dB است. این مورد، با روابط زیر نشان داده میشود.
توان تحویلی به بار، در فرکانس قطع، نصف میشود و میتوان پهنای باند (BW) منحنی پاسخ فرکانسی را با محدوده فرکانسی بین این نقاط نصف توان تعریف کرد.
از آنجایی که از $$20log_{10}(Av)$$ برای بهره ولتاژ و از $$20log_{10}(Ai)$$ برای بهره جریان استفاده میکنیم، عبارت لگاریتمی بهره توان به صورت $$10log_{10}(Ap)$$ خواهد بود. دقت کنید که وجود ضریب 20 به این معنی نیست که دو برابر 10 است، زیرا دسیبل واحد نرخ توان است و توان واقعی اندازهگیری شده نیست. همچنین بهره برحسب dB ممکن است مثبت یا منفی باشد که مقدار مثبت آن، تقویت و مقدار منفی آن تضعیف را نشان میدهد.
رابطه بین بهره ولتاژ، جریان و توان، در جدول زیر نشان داده شده است:
بهره ولتاژ حلقه باز تقویتکنندههای عملیاتی ($$A_{VO}$$)، به 1,000,000 یا 100dB میرسد.
اگر ورودی بک سیستم، 12mV و خروجی آن، 24mV باشد، مقدار ولتاژ خروجی را برحسب دسیبل محاسبه کنید.
توان خروجی یک تقویتکننده صوتی، در فرکانس 1kHz برابر با 10W و در فرکانس 10kHz معادل 1W است. تغییر dB توان را محاسبه کنید.
در این آموزش، دیدیم که چگونه میتوان محدوده فرکانسهای یک مدار الکترونیکی را با پاسخ فرکانسی آن تعیین کرد. پاسخ فرکانسی یک دستگاه یا مدار، عملکرد آن را در یک محدوده معین فرکانسی مشخص میکند و تغییرات بهره یا اندازه سیگنال را با تغییر فرکانس نشان میدهد.
نمودارهای بود، نمایش گرافیکی مشخصه پاسخ فرکانسی مدار هستند و میتوان از آنها در مسائل طراحی استفاده کرد. معمولاً توابع اندازه و فرکانس روی نمودارهای مجزایی رسم میشوند که محور x آنها با مقیاس لگاریتمی مدرج شده است.
پهنای باند، محدوده فرکانسهایی است که در آنها مدار بین فرکانس قطع پایین و بالا کار میکند. فرکانسهای قطع یا گوشه، نقاطی هستند که توان در آنجا به نصف حداکثر مقدار خود میرسد.
اغلب تقویتکنندهها و فیلترها، یک مشخصه پاسخ فرکانسی تخت دارند که در آن، پهنای باند یا باند گذر مدار، تخت است و در آن محدوده فرکانسی ثابت میماند. مدارهای تشدید، برای عبور دادن بخشی از محدوده فرکانسی طراحی شدهاند. این مدارها از مقاومت، سلف و خازن تشکیل میشوند که مقدار آنها با فرکانس تغییر میکند. نمودار پاسخ فرکانسی این مدارها مانند یک قله تیز است، زیرا پهنای باند آنها تحت تاثیر تشدید قرار میگیرد و به ضریب کیفیت (Q) مدار بستگی دارد. هرچه Q بیشتر باشد، پهنای باند کمتر است.
اگر مطالب بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط با آن بیشتر بدانید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 12 نفر
آیا این مطلب برای شما مفید بود؟
به عبارت دیگر فرکانس قطع در نمودار فرکانسی هست که بهره با اندازه ۳db افت می کند.پاسخ فركانسي چيست
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستمهای مخابراتی و سیستمهای کنترل کاربرد فراوانی دارد. بهطور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانسهای مورد نظر طراحی را عبور داده و سایر فرکانسها را حذف میکنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$ mathbf {H} ( omega ) $$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$ mathbf {H} ( omega ) $$ براساس $$ omega $$ است که از $$ omega =0$$ تا $$ omega = infty $$ تغییر میکند.
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را میتوان مطابق شکل ۱ نمایش داد.
تابع شبکه $$ mathbf {H} ( omega ) $$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$ mathbf {Y} ( omega ) $$ (ولتاژ یا جریان) به فازور ورودی $$ mathbf {X} ( omega ) $$ (منبع ولتاژ یا جریان) است.پاسخ فركانسي چيست
بنابراین، با فرض شرایط اولیه صفر، داریم:
از آنجایی که ورودی و خروجی میتوانند ولتاژ یا جریان هر نقطهای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:
که در آنها، پاییننویسهای $$i$$ و $$o$$ بهترتیب، مقادیر ورودی و خروجی را نشان میدهند. تابع $$ mathbf {H} ( omega ) $$، مختلط بوده و دارای اندازه $$ H ( omega ) $$ و زاویه فاز $$ phi $$ است ($$ mathbf {H} ( omega ) = H ( omega ) angle phi $$).
برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومتها، سلفها و خازنها با امپدانسهای $$R$$، $$ j omega L $$ و $$ 1/j omega C $$ بهدست میآوریم. پس از آن، از یکی از تکنیکهای تحلیل مدار برای بهدست آوردن یکی از معادلات (2) استفاده میکنیم. پاسخ فرکانسی را میتوان با رسم اندازه و فاز تابع شبکه برای فرکانسهای مختلف رسم کرد.
تابع شبکه $$ mathbf {H} ( omega ) $$ با نسبت چندجملهای صورت $$ mathbf {N} ( omega ) $$ و چندجملهای مخرج $$ mathbf {D} ( omega ) $$ قابل بیان است:
که در آن، $$ mathbf {N} ( omega ) $$ و $$ mathbf {D} ( omega ) $$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.
در نمایش $$ mathbf {H} ( omega ) $$ رابطه (۳) فرض شده که عاملهای مشترک صورت و مخرج حذف شدهاند. ریشههای $$ mathbf {N} ( omega ) =0 $$، صفرهای $$ mathbf {H} ( omega ) $$ نامیده شده و معمولاً بهصورت $$ j omega = z_1 , z_2 , cdots $$ نشان داده میشوند. بهطریق مشابه، ریشههای $$ mathbf {D} ( omega ) =0 $$ را قطبهای $$ mathbf {H} ( omega ) $$ مینامند و بهصورت $$ j omega = p_1 , p_2 , cdots $$ نشان میدهند.
برای اجتناب از انجام عملیات جبری پیچیده، $$ j omega $$ را با $$s$$ جایگزین میکنیم.
در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی میکنیم. ابتدا با مقیاس دسیبل آشنا میشویم.
رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظاممند برای بهدست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot) یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسیبل برای توصیف بهره آشنا باشیم.
از آنجایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:
در سیستمهای مخابراتی، بهره برحسب بِل (Bel) اندازهگیری میشود. از گذشته، بل برای اندازهگیری نسبت دو توان یا همان بهره توان $$G$$ استفاده میشود:
با کمک دسیبل (Decibel) میتوانیم اندازه کوچکتر را نیز بیان کنیم. دسیبل $$ 1/10$$ بل است و بهصورت زیر تعریف میشود:
وقتی $$ P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 , mathrm {dB}$$ است. اگر $$ P_2 = 2 P_1$$، بهره بهصورت زیر خواهد بود:
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:
روابط (۶) و (۷) نشان میدهند که چرا از لگاریتم استفاده بسیاری میشود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.
بهره $$G$$ را میتوان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آنگاه $$ P_1 = 0.5 V_1^2 / R_1 $$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را میتوان بهصورت زیر نوشت:
برای حالتی که $$ R_2 = R_1 $$، رابطه (۹) بهصورت زیر درمیآید:
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:
محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظاممندتر برای تعیین ویژگیهای مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمهلگاریتمی معرفی شده است که در آن، اندازه (برحسب دسیبل) براساس لگاریتم فرکانس رسم میشود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم میشود. این نمودارهای نیمهلگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots) نام دارند.
نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما میدهند و رسم آنها سادهتر است.
تابع شبکه را میتوان بهصورت زیر نوشت:
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:
بخش حقیقی $$ mathrm {ln} , mathbf {H} $$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان میدهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسیبل ($$mathrm {dB}$$) در مقابل فرکانس بیان میشود:
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسیبل آنها را نشان میدهد.
در یک نمودار فاز بُد، $$ phi$$ (برحسب درجه) در مقابل فرکانس رسم میشود. هردو نمودار اندازه و فاز، در مقیاس نیمهلگاریتمی رسم میشوند.
تابع شبکه (۳) را میتوان برحسب عاملهایی با بخشهای حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه بهصورت زیر است:
که صفرها و قطبهای $$ mathbf {H} (omega ) $$ را بهدست میدهد. نمایش $$ mathbf {H} (omega ) $$ در رابطه (15)، فرم استاندارد نامیده میشود. تابع $$ mathbf {H} (omega ) $$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرمهای مختلف و در ترکیبهای مختلف در تابع شبکه ظاهر میشوند. این عاملها عبارتند از:
برای بهدست آوردن نمودار بُد، عاملها را بهصورت جداگانه رسم، سپس آنها را با هم ترکیب میکنیم. در ادامه، نحوه رسم هریک از عاملهایی را که نام بردیم بیان میکنیم. این نمودارها را میتوان با تقریب بسیار خوبی رسم کرد.
اندازه و زاویه بهره $$K$$ بهترتیب $$ 20 log _{10} K $$ و $$ 0 ^ circ $$ است که هردو برای فرکانسهای مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شدهاند. اگر $$K$$ منفی باشد، انداز ه $$ 20 log _{10} |K| $$ باقی میماند، اما فاز $$ pm 180^ circ $$ خواهد شد.
برای صفر $$(j omega) $$ در مبدأ، اندازه $$20 log _{10} omega $$ و فاز $$90 ^ circ $$ است. این نمودارها در شکل ۴ رسم شدهاند. شیب نمودار اندازه، $$ 20 ,, mathrm {dB/ decade} $$ است، در حالی که مقدار فاز ثابت است.پاسخ فركانسي چيست
نمودار بُد قطب $$ (j omega )^ {-1} $$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$ -20 ,, mathrm {dB/ decade} $$ و فاز $$ -90 ^ circ $$ است. در حالت کلی، برای $$ (j omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$ 20N ,, mathrm{dB/decade} $$ است، در حالی که فاز $$ 90N $$ است.
برای صفر ساده $$(1+j omega / z_1)$$، اندازه $$ 20 ,, log _{10} |1+j omega / z_1 | $$ و فاز $$ tan ^ {-1} omega / z_1 $$ را داریم. در این حالت:
روابط اخیر نشان میدهند که میتوان برای مقادیر کوچک $$ omega $$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$ omega $$ بزرگ با یک خط راست با شیب $$ 20 ,, mathrm {dB/ decade} $$ تقریب زد. فرکانس $$ omega = z _1 $$ که در آن، دو خط مجانب به یکدیگر میرسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده میشود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شدهاند.
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$ omega = z_1$$ که مقدار اختلاف برابر است با $$20 , log _{10} |(1+j1)|=20, log _{10} sqrt {2} approx 3 , mathrm {dB}$$.
فاز $$ tan ^ {-1} ( frac{omega}{z_1}) $$ را میتوان بهصورت زیر نوشت:
در تقریب خط راست، فاز $$ phi approx 0 $$ را برای $$ omega le z_1/10 $$ و $$phi approx 45^ circ $$ را برای $$ omega = z_1$$ و $$ phi approx 90^ circ $$ را برای $$ omega ge 10 z_1 $$ در نظر میگیریم.
نمودارهای بُد برای قطب $$ 1/(1+ jomega / p_1 ) $$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$ omega = p_1 $$ که شیب اندازه $$ -20 , mathrm{dB/decade}$$ و شیب فاز $$-45 ^ circ $$ بر دهه (decade) است.
اندازه قطب درجه دوم $$ 1/ [1+ j2 zeta _2 omega / omega _n + (j omega / omega _n)^2] $$ برابر با $$ -20 log _{10} | 1+ j 2 zeta _2 omega / omega _n + j omega / omega _n + (j omega / omega _n)^2| $$ و فاز آن، معادلِ $$ tan ^ {-1} ( 2 zeta _2 omega / omega _n )/ (1- omega ^2 / omega _n^2) $$ است. برای فرکانسهای کوچک داریم:
و در فرکانسهای بزرگ:
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$ omega omega _n $$ که $$omega _n $$ فرکانس گوشه است.
شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان میدهد. نمودار دقیق، به ضریب میرایی $$ zeta _2 $$ و فرکانس گوشه $$ omega _n $$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابلتوجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.
نمودار فاز، خط راستی با شیب $$ -90 ^ circ $$ بر دهه است که از $$ omega _n $$ شروع شده و در $$ 10 omega _n $$ تمام میشود (شکل ۶ (ب)). مجدداً میبینیم که اختلاف نمودار دقیق و خط تقریبی بهدلیل ضریب میرایی است.
تقریب خطی نمودارهای اندازه و فاز برای قطبهای مرتبه دوم مشابه قطبهای تکراری $$ (1+j omega / omega _n ) ^{-2} $$ است. قطبهای تکراری، معادل قطب درجه دوم با $$ zeta _2 = 1 $$ هستند.
برای صفر درجه دوم، نمودارهای شکل ۶ معکوس میشوند، زیرا شیب نمودار اندازه $$ 40 , mathrm {dB/decade}$$ و شیب نمودار فاز $$ 90 ^ circ $$ بر دهه است.
جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان میدهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$ mathbf{H} ( omega ) $$ بهفرم رابطه (۱۵)، ابتدا فرکانسهای گوشه را در نمودار نیمهلگاریتمی مشخص میکنیم، سپس نمودار عاملها را با هم ترکیب میکنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیبها در هر فرکانس گوشه رسم میشود.
نمودارهای بُد تابع زیر را رسم کنید:
حل: ابتدا $$mathbf {H} (omega ) $$ را با تقسیم قطبها و صفرها بهفرم استاندارد مینویسیم:
بنابراین، اندازه و فاز بهصورت زیر هستند:
همانطور که میبینیم، دو فرکانس گوشه در $$ omega =2, 10 $$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 4 نفر
آیا این مطلب برای شما مفید بود؟
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستمهای مخابراتی و سیستمهای کنترل کاربرد فراوانی دارد. بهطور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانسهای مورد نظر طراحی را عبور داده و سایر فرکانسها را حذف میکنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$ mathbf {H} ( omega ) $$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$ mathbf {H} ( omega ) $$ براساس $$ omega $$ است که از $$ omega =0$$ تا $$ omega = infty $$ تغییر میکند.
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را میتوان مطابق شکل ۱ نمایش داد.
تابع شبکه $$ mathbf {H} ( omega ) $$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$ mathbf {Y} ( omega ) $$ (ولتاژ یا جریان) به فازور ورودی $$ mathbf {X} ( omega ) $$ (منبع ولتاژ یا جریان) است.پاسخ فركانسي چيست
بنابراین، با فرض شرایط اولیه صفر، داریم:
از آنجایی که ورودی و خروجی میتوانند ولتاژ یا جریان هر نقطهای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:
که در آنها، پاییننویسهای $$i$$ و $$o$$ بهترتیب، مقادیر ورودی و خروجی را نشان میدهند. تابع $$ mathbf {H} ( omega ) $$، مختلط بوده و دارای اندازه $$ H ( omega ) $$ و زاویه فاز $$ phi $$ است ($$ mathbf {H} ( omega ) = H ( omega ) angle phi $$).
برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومتها، سلفها و خازنها با امپدانسهای $$R$$، $$ j omega L $$ و $$ 1/j omega C $$ بهدست میآوریم. پس از آن، از یکی از تکنیکهای تحلیل مدار برای بهدست آوردن یکی از معادلات (2) استفاده میکنیم. پاسخ فرکانسی را میتوان با رسم اندازه و فاز تابع شبکه برای فرکانسهای مختلف رسم کرد.
تابع شبکه $$ mathbf {H} ( omega ) $$ با نسبت چندجملهای صورت $$ mathbf {N} ( omega ) $$ و چندجملهای مخرج $$ mathbf {D} ( omega ) $$ قابل بیان است:
که در آن، $$ mathbf {N} ( omega ) $$ و $$ mathbf {D} ( omega ) $$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.
در نمایش $$ mathbf {H} ( omega ) $$ رابطه (۳) فرض شده که عاملهای مشترک صورت و مخرج حذف شدهاند. ریشههای $$ mathbf {N} ( omega ) =0 $$، صفرهای $$ mathbf {H} ( omega ) $$ نامیده شده و معمولاً بهصورت $$ j omega = z_1 , z_2 , cdots $$ نشان داده میشوند. بهطریق مشابه، ریشههای $$ mathbf {D} ( omega ) =0 $$ را قطبهای $$ mathbf {H} ( omega ) $$ مینامند و بهصورت $$ j omega = p_1 , p_2 , cdots $$ نشان میدهند.
برای اجتناب از انجام عملیات جبری پیچیده، $$ j omega $$ را با $$s$$ جایگزین میکنیم.
در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی میکنیم. ابتدا با مقیاس دسیبل آشنا میشویم.
رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظاممند برای بهدست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot) یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسیبل برای توصیف بهره آشنا باشیم.
از آنجایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:
در سیستمهای مخابراتی، بهره برحسب بِل (Bel) اندازهگیری میشود. از گذشته، بل برای اندازهگیری نسبت دو توان یا همان بهره توان $$G$$ استفاده میشود:
با کمک دسیبل (Decibel) میتوانیم اندازه کوچکتر را نیز بیان کنیم. دسیبل $$ 1/10$$ بل است و بهصورت زیر تعریف میشود:
وقتی $$ P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 , mathrm {dB}$$ است. اگر $$ P_2 = 2 P_1$$، بهره بهصورت زیر خواهد بود:
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:
روابط (۶) و (۷) نشان میدهند که چرا از لگاریتم استفاده بسیاری میشود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.
بهره $$G$$ را میتوان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آنگاه $$ P_1 = 0.5 V_1^2 / R_1 $$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را میتوان بهصورت زیر نوشت:
برای حالتی که $$ R_2 = R_1 $$، رابطه (۹) بهصورت زیر درمیآید:
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:
محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظاممندتر برای تعیین ویژگیهای مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمهلگاریتمی معرفی شده است که در آن، اندازه (برحسب دسیبل) براساس لگاریتم فرکانس رسم میشود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم میشود. این نمودارهای نیمهلگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots) نام دارند.
نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما میدهند و رسم آنها سادهتر است.
تابع شبکه را میتوان بهصورت زیر نوشت:
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:
بخش حقیقی $$ mathrm {ln} , mathbf {H} $$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان میدهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسیبل ($$mathrm {dB}$$) در مقابل فرکانس بیان میشود:
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسیبل آنها را نشان میدهد.
در یک نمودار فاز بُد، $$ phi$$ (برحسب درجه) در مقابل فرکانس رسم میشود. هردو نمودار اندازه و فاز، در مقیاس نیمهلگاریتمی رسم میشوند.
تابع شبکه (۳) را میتوان برحسب عاملهایی با بخشهای حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه بهصورت زیر است:
که صفرها و قطبهای $$ mathbf {H} (omega ) $$ را بهدست میدهد. نمایش $$ mathbf {H} (omega ) $$ در رابطه (15)، فرم استاندارد نامیده میشود. تابع $$ mathbf {H} (omega ) $$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرمهای مختلف و در ترکیبهای مختلف در تابع شبکه ظاهر میشوند. این عاملها عبارتند از:
برای بهدست آوردن نمودار بُد، عاملها را بهصورت جداگانه رسم، سپس آنها را با هم ترکیب میکنیم. در ادامه، نحوه رسم هریک از عاملهایی را که نام بردیم بیان میکنیم. این نمودارها را میتوان با تقریب بسیار خوبی رسم کرد.
اندازه و زاویه بهره $$K$$ بهترتیب $$ 20 log _{10} K $$ و $$ 0 ^ circ $$ است که هردو برای فرکانسهای مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شدهاند. اگر $$K$$ منفی باشد، انداز ه $$ 20 log _{10} |K| $$ باقی میماند، اما فاز $$ pm 180^ circ $$ خواهد شد.
برای صفر $$(j omega) $$ در مبدأ، اندازه $$20 log _{10} omega $$ و فاز $$90 ^ circ $$ است. این نمودارها در شکل ۴ رسم شدهاند. شیب نمودار اندازه، $$ 20 ,, mathrm {dB/ decade} $$ است، در حالی که مقدار فاز ثابت است.پاسخ فركانسي چيست
نمودار بُد قطب $$ (j omega )^ {-1} $$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$ -20 ,, mathrm {dB/ decade} $$ و فاز $$ -90 ^ circ $$ است. در حالت کلی، برای $$ (j omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$ 20N ,, mathrm{dB/decade} $$ است، در حالی که فاز $$ 90N $$ است.
برای صفر ساده $$(1+j omega / z_1)$$، اندازه $$ 20 ,, log _{10} |1+j omega / z_1 | $$ و فاز $$ tan ^ {-1} omega / z_1 $$ را داریم. در این حالت:
روابط اخیر نشان میدهند که میتوان برای مقادیر کوچک $$ omega $$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$ omega $$ بزرگ با یک خط راست با شیب $$ 20 ,, mathrm {dB/ decade} $$ تقریب زد. فرکانس $$ omega = z _1 $$ که در آن، دو خط مجانب به یکدیگر میرسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده میشود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شدهاند.
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$ omega = z_1$$ که مقدار اختلاف برابر است با $$20 , log _{10} |(1+j1)|=20, log _{10} sqrt {2} approx 3 , mathrm {dB}$$.
فاز $$ tan ^ {-1} ( frac{omega}{z_1}) $$ را میتوان بهصورت زیر نوشت:
در تقریب خط راست، فاز $$ phi approx 0 $$ را برای $$ omega le z_1/10 $$ و $$phi approx 45^ circ $$ را برای $$ omega = z_1$$ و $$ phi approx 90^ circ $$ را برای $$ omega ge 10 z_1 $$ در نظر میگیریم.
نمودارهای بُد برای قطب $$ 1/(1+ jomega / p_1 ) $$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$ omega = p_1 $$ که شیب اندازه $$ -20 , mathrm{dB/decade}$$ و شیب فاز $$-45 ^ circ $$ بر دهه (decade) است.
اندازه قطب درجه دوم $$ 1/ [1+ j2 zeta _2 omega / omega _n + (j omega / omega _n)^2] $$ برابر با $$ -20 log _{10} | 1+ j 2 zeta _2 omega / omega _n + j omega / omega _n + (j omega / omega _n)^2| $$ و فاز آن، معادلِ $$ tan ^ {-1} ( 2 zeta _2 omega / omega _n )/ (1- omega ^2 / omega _n^2) $$ است. برای فرکانسهای کوچک داریم:
و در فرکانسهای بزرگ:
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$ omega omega _n $$ که $$omega _n $$ فرکانس گوشه است.
شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان میدهد. نمودار دقیق، به ضریب میرایی $$ zeta _2 $$ و فرکانس گوشه $$ omega _n $$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابلتوجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.
نمودار فاز، خط راستی با شیب $$ -90 ^ circ $$ بر دهه است که از $$ omega _n $$ شروع شده و در $$ 10 omega _n $$ تمام میشود (شکل ۶ (ب)). مجدداً میبینیم که اختلاف نمودار دقیق و خط تقریبی بهدلیل ضریب میرایی است.
تقریب خطی نمودارهای اندازه و فاز برای قطبهای مرتبه دوم مشابه قطبهای تکراری $$ (1+j omega / omega _n ) ^{-2} $$ است. قطبهای تکراری، معادل قطب درجه دوم با $$ zeta _2 = 1 $$ هستند.
برای صفر درجه دوم، نمودارهای شکل ۶ معکوس میشوند، زیرا شیب نمودار اندازه $$ 40 , mathrm {dB/decade}$$ و شیب نمودار فاز $$ 90 ^ circ $$ بر دهه است.
جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان میدهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$ mathbf{H} ( omega ) $$ بهفرم رابطه (۱۵)، ابتدا فرکانسهای گوشه را در نمودار نیمهلگاریتمی مشخص میکنیم، سپس نمودار عاملها را با هم ترکیب میکنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیبها در هر فرکانس گوشه رسم میشود.
نمودارهای بُد تابع زیر را رسم کنید:
حل: ابتدا $$mathbf {H} (omega ) $$ را با تقسیم قطبها و صفرها بهفرم استاندارد مینویسیم:
بنابراین، اندازه و فاز بهصورت زیر هستند:
همانطور که میبینیم، دو فرکانس گوشه در $$ omega =2, 10 $$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 4 نفر
آیا این مطلب برای شما مفید بود؟
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستمهای مخابراتی و سیستمهای کنترل کاربرد فراوانی دارد. بهطور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانسهای مورد نظر طراحی را عبور داده و سایر فرکانسها را حذف میکنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$ mathbf {H} ( omega ) $$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$ mathbf {H} ( omega ) $$ براساس $$ omega $$ است که از $$ omega =0$$ تا $$ omega = infty $$ تغییر میکند.
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را میتوان مطابق شکل ۱ نمایش داد.
تابع شبکه $$ mathbf {H} ( omega ) $$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$ mathbf {Y} ( omega ) $$ (ولتاژ یا جریان) به فازور ورودی $$ mathbf {X} ( omega ) $$ (منبع ولتاژ یا جریان) است.پاسخ فركانسي چيست
بنابراین، با فرض شرایط اولیه صفر، داریم:
از آنجایی که ورودی و خروجی میتوانند ولتاژ یا جریان هر نقطهای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:
که در آنها، پاییننویسهای $$i$$ و $$o$$ بهترتیب، مقادیر ورودی و خروجی را نشان میدهند. تابع $$ mathbf {H} ( omega ) $$، مختلط بوده و دارای اندازه $$ H ( omega ) $$ و زاویه فاز $$ phi $$ است ($$ mathbf {H} ( omega ) = H ( omega ) angle phi $$).
برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومتها، سلفها و خازنها با امپدانسهای $$R$$، $$ j omega L $$ و $$ 1/j omega C $$ بهدست میآوریم. پس از آن، از یکی از تکنیکهای تحلیل مدار برای بهدست آوردن یکی از معادلات (2) استفاده میکنیم. پاسخ فرکانسی را میتوان با رسم اندازه و فاز تابع شبکه برای فرکانسهای مختلف رسم کرد.
تابع شبکه $$ mathbf {H} ( omega ) $$ با نسبت چندجملهای صورت $$ mathbf {N} ( omega ) $$ و چندجملهای مخرج $$ mathbf {D} ( omega ) $$ قابل بیان است:
که در آن، $$ mathbf {N} ( omega ) $$ و $$ mathbf {D} ( omega ) $$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.
در نمایش $$ mathbf {H} ( omega ) $$ رابطه (۳) فرض شده که عاملهای مشترک صورت و مخرج حذف شدهاند. ریشههای $$ mathbf {N} ( omega ) =0 $$، صفرهای $$ mathbf {H} ( omega ) $$ نامیده شده و معمولاً بهصورت $$ j omega = z_1 , z_2 , cdots $$ نشان داده میشوند. بهطریق مشابه، ریشههای $$ mathbf {D} ( omega ) =0 $$ را قطبهای $$ mathbf {H} ( omega ) $$ مینامند و بهصورت $$ j omega = p_1 , p_2 , cdots $$ نشان میدهند.
برای اجتناب از انجام عملیات جبری پیچیده، $$ j omega $$ را با $$s$$ جایگزین میکنیم.
در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی میکنیم. ابتدا با مقیاس دسیبل آشنا میشویم.
رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظاممند برای بهدست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot) یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسیبل برای توصیف بهره آشنا باشیم.
از آنجایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:
در سیستمهای مخابراتی، بهره برحسب بِل (Bel) اندازهگیری میشود. از گذشته، بل برای اندازهگیری نسبت دو توان یا همان بهره توان $$G$$ استفاده میشود:
با کمک دسیبل (Decibel) میتوانیم اندازه کوچکتر را نیز بیان کنیم. دسیبل $$ 1/10$$ بل است و بهصورت زیر تعریف میشود:
وقتی $$ P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 , mathrm {dB}$$ است. اگر $$ P_2 = 2 P_1$$، بهره بهصورت زیر خواهد بود:
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:
روابط (۶) و (۷) نشان میدهند که چرا از لگاریتم استفاده بسیاری میشود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.
بهره $$G$$ را میتوان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آنگاه $$ P_1 = 0.5 V_1^2 / R_1 $$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را میتوان بهصورت زیر نوشت:
برای حالتی که $$ R_2 = R_1 $$، رابطه (۹) بهصورت زیر درمیآید:
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:
محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظاممندتر برای تعیین ویژگیهای مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمهلگاریتمی معرفی شده است که در آن، اندازه (برحسب دسیبل) براساس لگاریتم فرکانس رسم میشود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم میشود. این نمودارهای نیمهلگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots) نام دارند.
نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما میدهند و رسم آنها سادهتر است.
تابع شبکه را میتوان بهصورت زیر نوشت:
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:
بخش حقیقی $$ mathrm {ln} , mathbf {H} $$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان میدهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسیبل ($$mathrm {dB}$$) در مقابل فرکانس بیان میشود:
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسیبل آنها را نشان میدهد.
در یک نمودار فاز بُد، $$ phi$$ (برحسب درجه) در مقابل فرکانس رسم میشود. هردو نمودار اندازه و فاز، در مقیاس نیمهلگاریتمی رسم میشوند.
تابع شبکه (۳) را میتوان برحسب عاملهایی با بخشهای حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه بهصورت زیر است:
که صفرها و قطبهای $$ mathbf {H} (omega ) $$ را بهدست میدهد. نمایش $$ mathbf {H} (omega ) $$ در رابطه (15)، فرم استاندارد نامیده میشود. تابع $$ mathbf {H} (omega ) $$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرمهای مختلف و در ترکیبهای مختلف در تابع شبکه ظاهر میشوند. این عاملها عبارتند از:
برای بهدست آوردن نمودار بُد، عاملها را بهصورت جداگانه رسم، سپس آنها را با هم ترکیب میکنیم. در ادامه، نحوه رسم هریک از عاملهایی را که نام بردیم بیان میکنیم. این نمودارها را میتوان با تقریب بسیار خوبی رسم کرد.
اندازه و زاویه بهره $$K$$ بهترتیب $$ 20 log _{10} K $$ و $$ 0 ^ circ $$ است که هردو برای فرکانسهای مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شدهاند. اگر $$K$$ منفی باشد، انداز ه $$ 20 log _{10} |K| $$ باقی میماند، اما فاز $$ pm 180^ circ $$ خواهد شد.
برای صفر $$(j omega) $$ در مبدأ، اندازه $$20 log _{10} omega $$ و فاز $$90 ^ circ $$ است. این نمودارها در شکل ۴ رسم شدهاند. شیب نمودار اندازه، $$ 20 ,, mathrm {dB/ decade} $$ است، در حالی که مقدار فاز ثابت است.پاسخ فركانسي چيست
نمودار بُد قطب $$ (j omega )^ {-1} $$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$ -20 ,, mathrm {dB/ decade} $$ و فاز $$ -90 ^ circ $$ است. در حالت کلی، برای $$ (j omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$ 20N ,, mathrm{dB/decade} $$ است، در حالی که فاز $$ 90N $$ است.
برای صفر ساده $$(1+j omega / z_1)$$، اندازه $$ 20 ,, log _{10} |1+j omega / z_1 | $$ و فاز $$ tan ^ {-1} omega / z_1 $$ را داریم. در این حالت:
روابط اخیر نشان میدهند که میتوان برای مقادیر کوچک $$ omega $$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$ omega $$ بزرگ با یک خط راست با شیب $$ 20 ,, mathrm {dB/ decade} $$ تقریب زد. فرکانس $$ omega = z _1 $$ که در آن، دو خط مجانب به یکدیگر میرسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده میشود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شدهاند.
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$ omega = z_1$$ که مقدار اختلاف برابر است با $$20 , log _{10} |(1+j1)|=20, log _{10} sqrt {2} approx 3 , mathrm {dB}$$.
فاز $$ tan ^ {-1} ( frac{omega}{z_1}) $$ را میتوان بهصورت زیر نوشت:
در تقریب خط راست، فاز $$ phi approx 0 $$ را برای $$ omega le z_1/10 $$ و $$phi approx 45^ circ $$ را برای $$ omega = z_1$$ و $$ phi approx 90^ circ $$ را برای $$ omega ge 10 z_1 $$ در نظر میگیریم.
نمودارهای بُد برای قطب $$ 1/(1+ jomega / p_1 ) $$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$ omega = p_1 $$ که شیب اندازه $$ -20 , mathrm{dB/decade}$$ و شیب فاز $$-45 ^ circ $$ بر دهه (decade) است.
اندازه قطب درجه دوم $$ 1/ [1+ j2 zeta _2 omega / omega _n + (j omega / omega _n)^2] $$ برابر با $$ -20 log _{10} | 1+ j 2 zeta _2 omega / omega _n + j omega / omega _n + (j omega / omega _n)^2| $$ و فاز آن، معادلِ $$ tan ^ {-1} ( 2 zeta _2 omega / omega _n )/ (1- omega ^2 / omega _n^2) $$ است. برای فرکانسهای کوچک داریم:
و در فرکانسهای بزرگ:
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$ omega omega _n $$ که $$omega _n $$ فرکانس گوشه است.
شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان میدهد. نمودار دقیق، به ضریب میرایی $$ zeta _2 $$ و فرکانس گوشه $$ omega _n $$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابلتوجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.
نمودار فاز، خط راستی با شیب $$ -90 ^ circ $$ بر دهه است که از $$ omega _n $$ شروع شده و در $$ 10 omega _n $$ تمام میشود (شکل ۶ (ب)). مجدداً میبینیم که اختلاف نمودار دقیق و خط تقریبی بهدلیل ضریب میرایی است.
تقریب خطی نمودارهای اندازه و فاز برای قطبهای مرتبه دوم مشابه قطبهای تکراری $$ (1+j omega / omega _n ) ^{-2} $$ است. قطبهای تکراری، معادل قطب درجه دوم با $$ zeta _2 = 1 $$ هستند.
برای صفر درجه دوم، نمودارهای شکل ۶ معکوس میشوند، زیرا شیب نمودار اندازه $$ 40 , mathrm {dB/decade}$$ و شیب نمودار فاز $$ 90 ^ circ $$ بر دهه است.
جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان میدهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$ mathbf{H} ( omega ) $$ بهفرم رابطه (۱۵)، ابتدا فرکانسهای گوشه را در نمودار نیمهلگاریتمی مشخص میکنیم، سپس نمودار عاملها را با هم ترکیب میکنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیبها در هر فرکانس گوشه رسم میشود.
نمودارهای بُد تابع زیر را رسم کنید:
حل: ابتدا $$mathbf {H} (omega ) $$ را با تقسیم قطبها و صفرها بهفرم استاندارد مینویسیم:
بنابراین، اندازه و فاز بهصورت زیر هستند:
همانطور که میبینیم، دو فرکانس گوشه در $$ omega =2, 10 $$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 4 نفر
آیا این مطلب برای شما مفید بود؟
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستمهای مخابراتی و سیستمهای کنترل کاربرد فراوانی دارد. بهطور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانسهای مورد نظر طراحی را عبور داده و سایر فرکانسها را حذف میکنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$ mathbf {H} ( omega ) $$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$ mathbf {H} ( omega ) $$ براساس $$ omega $$ است که از $$ omega =0$$ تا $$ omega = infty $$ تغییر میکند.
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را میتوان مطابق شکل ۱ نمایش داد.
تابع شبکه $$ mathbf {H} ( omega ) $$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$ mathbf {Y} ( omega ) $$ (ولتاژ یا جریان) به فازور ورودی $$ mathbf {X} ( omega ) $$ (منبع ولتاژ یا جریان) است.پاسخ فركانسي چيست
بنابراین، با فرض شرایط اولیه صفر، داریم:
از آنجایی که ورودی و خروجی میتوانند ولتاژ یا جریان هر نقطهای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:
که در آنها، پاییننویسهای $$i$$ و $$o$$ بهترتیب، مقادیر ورودی و خروجی را نشان میدهند. تابع $$ mathbf {H} ( omega ) $$، مختلط بوده و دارای اندازه $$ H ( omega ) $$ و زاویه فاز $$ phi $$ است ($$ mathbf {H} ( omega ) = H ( omega ) angle phi $$).
برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومتها، سلفها و خازنها با امپدانسهای $$R$$، $$ j omega L $$ و $$ 1/j omega C $$ بهدست میآوریم. پس از آن، از یکی از تکنیکهای تحلیل مدار برای بهدست آوردن یکی از معادلات (2) استفاده میکنیم. پاسخ فرکانسی را میتوان با رسم اندازه و فاز تابع شبکه برای فرکانسهای مختلف رسم کرد.
تابع شبکه $$ mathbf {H} ( omega ) $$ با نسبت چندجملهای صورت $$ mathbf {N} ( omega ) $$ و چندجملهای مخرج $$ mathbf {D} ( omega ) $$ قابل بیان است:
که در آن، $$ mathbf {N} ( omega ) $$ و $$ mathbf {D} ( omega ) $$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.
در نمایش $$ mathbf {H} ( omega ) $$ رابطه (۳) فرض شده که عاملهای مشترک صورت و مخرج حذف شدهاند. ریشههای $$ mathbf {N} ( omega ) =0 $$، صفرهای $$ mathbf {H} ( omega ) $$ نامیده شده و معمولاً بهصورت $$ j omega = z_1 , z_2 , cdots $$ نشان داده میشوند. بهطریق مشابه، ریشههای $$ mathbf {D} ( omega ) =0 $$ را قطبهای $$ mathbf {H} ( omega ) $$ مینامند و بهصورت $$ j omega = p_1 , p_2 , cdots $$ نشان میدهند.
برای اجتناب از انجام عملیات جبری پیچیده، $$ j omega $$ را با $$s$$ جایگزین میکنیم.
در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی میکنیم. ابتدا با مقیاس دسیبل آشنا میشویم.
رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظاممند برای بهدست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot) یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسیبل برای توصیف بهره آشنا باشیم.
از آنجایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:
در سیستمهای مخابراتی، بهره برحسب بِل (Bel) اندازهگیری میشود. از گذشته، بل برای اندازهگیری نسبت دو توان یا همان بهره توان $$G$$ استفاده میشود:
با کمک دسیبل (Decibel) میتوانیم اندازه کوچکتر را نیز بیان کنیم. دسیبل $$ 1/10$$ بل است و بهصورت زیر تعریف میشود:
وقتی $$ P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 , mathrm {dB}$$ است. اگر $$ P_2 = 2 P_1$$، بهره بهصورت زیر خواهد بود:
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:
روابط (۶) و (۷) نشان میدهند که چرا از لگاریتم استفاده بسیاری میشود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.
بهره $$G$$ را میتوان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آنگاه $$ P_1 = 0.5 V_1^2 / R_1 $$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را میتوان بهصورت زیر نوشت:
برای حالتی که $$ R_2 = R_1 $$، رابطه (۹) بهصورت زیر درمیآید:
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:
محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظاممندتر برای تعیین ویژگیهای مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمهلگاریتمی معرفی شده است که در آن، اندازه (برحسب دسیبل) براساس لگاریتم فرکانس رسم میشود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم میشود. این نمودارهای نیمهلگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots) نام دارند.
نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما میدهند و رسم آنها سادهتر است.
تابع شبکه را میتوان بهصورت زیر نوشت:
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:
بخش حقیقی $$ mathrm {ln} , mathbf {H} $$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان میدهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسیبل ($$mathrm {dB}$$) در مقابل فرکانس بیان میشود:
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسیبل آنها را نشان میدهد.
در یک نمودار فاز بُد، $$ phi$$ (برحسب درجه) در مقابل فرکانس رسم میشود. هردو نمودار اندازه و فاز، در مقیاس نیمهلگاریتمی رسم میشوند.
تابع شبکه (۳) را میتوان برحسب عاملهایی با بخشهای حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه بهصورت زیر است:
که صفرها و قطبهای $$ mathbf {H} (omega ) $$ را بهدست میدهد. نمایش $$ mathbf {H} (omega ) $$ در رابطه (15)، فرم استاندارد نامیده میشود. تابع $$ mathbf {H} (omega ) $$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرمهای مختلف و در ترکیبهای مختلف در تابع شبکه ظاهر میشوند. این عاملها عبارتند از:
برای بهدست آوردن نمودار بُد، عاملها را بهصورت جداگانه رسم، سپس آنها را با هم ترکیب میکنیم. در ادامه، نحوه رسم هریک از عاملهایی را که نام بردیم بیان میکنیم. این نمودارها را میتوان با تقریب بسیار خوبی رسم کرد.
اندازه و زاویه بهره $$K$$ بهترتیب $$ 20 log _{10} K $$ و $$ 0 ^ circ $$ است که هردو برای فرکانسهای مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شدهاند. اگر $$K$$ منفی باشد، انداز ه $$ 20 log _{10} |K| $$ باقی میماند، اما فاز $$ pm 180^ circ $$ خواهد شد.
برای صفر $$(j omega) $$ در مبدأ، اندازه $$20 log _{10} omega $$ و فاز $$90 ^ circ $$ است. این نمودارها در شکل ۴ رسم شدهاند. شیب نمودار اندازه، $$ 20 ,, mathrm {dB/ decade} $$ است، در حالی که مقدار فاز ثابت است.پاسخ فركانسي چيست
نمودار بُد قطب $$ (j omega )^ {-1} $$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$ -20 ,, mathrm {dB/ decade} $$ و فاز $$ -90 ^ circ $$ است. در حالت کلی، برای $$ (j omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$ 20N ,, mathrm{dB/decade} $$ است، در حالی که فاز $$ 90N $$ است.
برای صفر ساده $$(1+j omega / z_1)$$، اندازه $$ 20 ,, log _{10} |1+j omega / z_1 | $$ و فاز $$ tan ^ {-1} omega / z_1 $$ را داریم. در این حالت:
روابط اخیر نشان میدهند که میتوان برای مقادیر کوچک $$ omega $$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$ omega $$ بزرگ با یک خط راست با شیب $$ 20 ,, mathrm {dB/ decade} $$ تقریب زد. فرکانس $$ omega = z _1 $$ که در آن، دو خط مجانب به یکدیگر میرسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده میشود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شدهاند.
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$ omega = z_1$$ که مقدار اختلاف برابر است با $$20 , log _{10} |(1+j1)|=20, log _{10} sqrt {2} approx 3 , mathrm {dB}$$.
فاز $$ tan ^ {-1} ( frac{omega}{z_1}) $$ را میتوان بهصورت زیر نوشت:
در تقریب خط راست، فاز $$ phi approx 0 $$ را برای $$ omega le z_1/10 $$ و $$phi approx 45^ circ $$ را برای $$ omega = z_1$$ و $$ phi approx 90^ circ $$ را برای $$ omega ge 10 z_1 $$ در نظر میگیریم.
نمودارهای بُد برای قطب $$ 1/(1+ jomega / p_1 ) $$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$ omega = p_1 $$ که شیب اندازه $$ -20 , mathrm{dB/decade}$$ و شیب فاز $$-45 ^ circ $$ بر دهه (decade) است.
اندازه قطب درجه دوم $$ 1/ [1+ j2 zeta _2 omega / omega _n + (j omega / omega _n)^2] $$ برابر با $$ -20 log _{10} | 1+ j 2 zeta _2 omega / omega _n + j omega / omega _n + (j omega / omega _n)^2| $$ و فاز آن، معادلِ $$ tan ^ {-1} ( 2 zeta _2 omega / omega _n )/ (1- omega ^2 / omega _n^2) $$ است. برای فرکانسهای کوچک داریم:
و در فرکانسهای بزرگ:
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$ omega omega _n $$ که $$omega _n $$ فرکانس گوشه است.
شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان میدهد. نمودار دقیق، به ضریب میرایی $$ zeta _2 $$ و فرکانس گوشه $$ omega _n $$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابلتوجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.
نمودار فاز، خط راستی با شیب $$ -90 ^ circ $$ بر دهه است که از $$ omega _n $$ شروع شده و در $$ 10 omega _n $$ تمام میشود (شکل ۶ (ب)). مجدداً میبینیم که اختلاف نمودار دقیق و خط تقریبی بهدلیل ضریب میرایی است.
تقریب خطی نمودارهای اندازه و فاز برای قطبهای مرتبه دوم مشابه قطبهای تکراری $$ (1+j omega / omega _n ) ^{-2} $$ است. قطبهای تکراری، معادل قطب درجه دوم با $$ zeta _2 = 1 $$ هستند.
برای صفر درجه دوم، نمودارهای شکل ۶ معکوس میشوند، زیرا شیب نمودار اندازه $$ 40 , mathrm {dB/decade}$$ و شیب نمودار فاز $$ 90 ^ circ $$ بر دهه است.
جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان میدهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$ mathbf{H} ( omega ) $$ بهفرم رابطه (۱۵)، ابتدا فرکانسهای گوشه را در نمودار نیمهلگاریتمی مشخص میکنیم، سپس نمودار عاملها را با هم ترکیب میکنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیبها در هر فرکانس گوشه رسم میشود.
نمودارهای بُد تابع زیر را رسم کنید:
حل: ابتدا $$mathbf {H} (omega ) $$ را با تقسیم قطبها و صفرها بهفرم استاندارد مینویسیم:
بنابراین، اندازه و فاز بهصورت زیر هستند:
همانطور که میبینیم، دو فرکانس گوشه در $$ omega =2, 10 $$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 4 نفر
آیا این مطلب برای شما مفید بود؟
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
پاسخ فرکانسی حالت دائمی سینوسی مدار، در موارد مختلفی از جمله سیستمهای مخابراتی و سیستمهای کنترل کاربرد فراوانی دارد. بهطور خاص، یکی از کاربردهای پاسخ فرکانسی در فیلترها است که فرکانسهای مورد نظر طراحی را عبور داده و سایر فرکانسها را حذف میکنند. در این آموزش، ابتدا تابع شبکه را معرفی کرده، سپس با استفاده از آن، رسم پاسخ فرکانسی را در قالب نمودارهای بُد بیان خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
تابع تبدیل (Transfer Function) یا تابع شبکه (Network Function) $$ mathbf {H} ( omega ) $$، یک ابزار تحلیلی برای یافتن پاسخ فرکانسی مدار است. در حقیقت، پاسخ فرکانسی یک مدار، نمودار تابع شبکه $$ mathbf {H} ( omega ) $$ براساس $$ omega $$ است که از $$ omega =0$$ تا $$ omega = infty $$ تغییر میکند.
تابع شبکه، نسبت وابسته به فرکانسِ یک تابع خروجی به یک تابع ورودی است. در حالت کلی، یک شبکه خطی را میتوان مطابق شکل ۱ نمایش داد.
تابع شبکه $$ mathbf {H} ( omega ) $$ مدار، نسبت وابسته به فرکانسِ فازور خروجی $$ mathbf {Y} ( omega ) $$ (ولتاژ یا جریان) به فازور ورودی $$ mathbf {X} ( omega ) $$ (منبع ولتاژ یا جریان) است.پاسخ فركانسي چيست
بنابراین، با فرض شرایط اولیه صفر، داریم:
از آنجایی که ورودی و خروجی میتوانند ولتاژ یا جریان هر نقطهای از مدار باشند، چهار تابع شبکه ممکن وجود دارد:
که در آنها، پاییننویسهای $$i$$ و $$o$$ بهترتیب، مقادیر ورودی و خروجی را نشان میدهند. تابع $$ mathbf {H} ( omega ) $$، مختلط بوده و دارای اندازه $$ H ( omega ) $$ و زاویه فاز $$ phi $$ است ($$ mathbf {H} ( omega ) = H ( omega ) angle phi $$).
برای نوشتن تابع شبکه، ابتدا معادل حوزه فرکانس مدار را با جایگزینی مقاومتها، سلفها و خازنها با امپدانسهای $$R$$، $$ j omega L $$ و $$ 1/j omega C $$ بهدست میآوریم. پس از آن، از یکی از تکنیکهای تحلیل مدار برای بهدست آوردن یکی از معادلات (2) استفاده میکنیم. پاسخ فرکانسی را میتوان با رسم اندازه و فاز تابع شبکه برای فرکانسهای مختلف رسم کرد.
تابع شبکه $$ mathbf {H} ( omega ) $$ با نسبت چندجملهای صورت $$ mathbf {N} ( omega ) $$ و چندجملهای مخرج $$ mathbf {D} ( omega ) $$ قابل بیان است:
که در آن، $$ mathbf {N} ( omega ) $$ و $$ mathbf {D} ( omega ) $$ لزوماً توصیفات یکسانی برای توابع ورودی و خروجی ندارند.
در نمایش $$ mathbf {H} ( omega ) $$ رابطه (۳) فرض شده که عاملهای مشترک صورت و مخرج حذف شدهاند. ریشههای $$ mathbf {N} ( omega ) =0 $$، صفرهای $$ mathbf {H} ( omega ) $$ نامیده شده و معمولاً بهصورت $$ j omega = z_1 , z_2 , cdots $$ نشان داده میشوند. بهطریق مشابه، ریشههای $$ mathbf {D} ( omega ) =0 $$ را قطبهای $$ mathbf {H} ( omega ) $$ مینامند و بهصورت $$ j omega = p_1 , p_2 , cdots $$ نشان میدهند.
برای اجتناب از انجام عملیات جبری پیچیده، $$ j omega $$ را با $$s$$ جایگزین میکنیم.
در ادامه، نحوه رسم پاسخ فرکانسی مدار را بررسی میکنیم. ابتدا با مقیاس دسیبل آشنا میشویم.
رسم سریع اندازه و فاز تابع شبکه، همیشه کار آسانی نیست. یک راه نظاممند برای بهدست آوردن پاسخ فرکانسی، استفاده از «نمودار بُد» (Bode Plot) یا بود یا بودی یا بودا است. قبل از پرداختن به نمودارهای بُد، لازم است با موضوع مهم استفاده از لگاریتم و دسیبل برای توصیف بهره آشنا باشیم.
از آنجایی که نمودارهای بُد براساس لگاریتم هستند، لازم است روابط زیر را در ذهن داشته باشیم:
در سیستمهای مخابراتی، بهره برحسب بِل (Bel) اندازهگیری میشود. از گذشته، بل برای اندازهگیری نسبت دو توان یا همان بهره توان $$G$$ استفاده میشود:
با کمک دسیبل (Decibel) میتوانیم اندازه کوچکتر را نیز بیان کنیم. دسیبل $$ 1/10$$ بل است و بهصورت زیر تعریف میشود:
وقتی $$ P_1 = P_2$$، تغییری در توان حاصل نشده و بهره برابر با $$0 , mathrm {dB}$$ است. اگر $$ P_2 = 2 P_1$$، بهره بهصورت زیر خواهد بود:
و وقتی $$P_2 = 0.5 P_1$$، بهره برابر است با:
روابط (۶) و (۷) نشان میدهند که چرا از لگاریتم استفاده بسیاری میشود. لگاریتم معکوس یک کمیت، قرینه لگاریتم آن کمیت است.
بهره $$G$$ را میتوان براساس نسبت ولتاژ یا جریان نیز بیان کرد. برای این کار، شبکه شکل ۲ را در نظر بگیرید.
اگر $$P_1$$ توان ورودی و $$P_2$$ توان خروجی (بار)، $$R_1$$ مقاومت ورودی و $$R_2$$ مقاومت بار باشد، آنگاه $$ P_1 = 0.5 V_1^2 / R_1 $$ و $$P_2 = 0.5 V_2^2 / R_2$$ و رابطه (۵) را میتوان بهصورت زیر نوشت:
برای حالتی که $$ R_2 = R_1 $$، رابطه (۹) بهصورت زیر درمیآید:
از سوی دیگر، اگر $$P_1 = I_1^2 R_1$$ و $$P_2 = I_2^2 R_2$$ و $$R_1=R_2$$ باشد، داریم:
درباره روابط (5)، (10) و (۱۱) سه نکته مهم وجود دارد:
محدوده فرکانسی لازم در پاسخ فرکانسی، اغلب گسترده است و استفاده از یک مقیاس خطی برای محور فرکانس، کار دشواری است. همچنین، یک راه نظاممندتر برای تعیین ویژگیهای مهم نموادرهای اندازه و فاز تابع شبکه وجود دارد. به این دلایل، یک روش استاندارد برای رسم تابع شبکه روی دو نمودار نیمهلگاریتمی معرفی شده است که در آن، اندازه (برحسب دسیبل) براساس لگاریتم فرکانس رسم میشود. همچنین، در یک نمودار دیگر، فاز (برحسب درجه) براساس لگاریتم فرکانس رسم میشود. این نمودارهای نیمهلگاریتمی از تابع شبکه، «نمودارهای بُد» (Bode Plots) نام دارند.
نمودارهای بُد، همان اطلاعات نمودارهای غیرلگاریتمی را به ما میدهند و رسم آنها سادهتر است.
تابع شبکه را میتوان بهصورت زیر نوشت:
با لگاریتم طبیعی گرفتن از دو طرف رابطه اخیر، داریم:
بخش حقیقی $$ mathrm {ln} , mathbf {H} $$، تابعی از اندازه است، در حالی که بخش موهومی، فاز را نشان میدهد. در یک نمودار اندازه بُد، بهره زیر برحسب دسیبل ($$mathrm {dB}$$) در مقابل فرکانس بیان میشود:
جدول ۱ تعدادی از مقادیر $$H$$ و معادل دسیبل آنها را نشان میدهد.
در یک نمودار فاز بُد، $$ phi$$ (برحسب درجه) در مقابل فرکانس رسم میشود. هردو نمودار اندازه و فاز، در مقیاس نیمهلگاریتمی رسم میشوند.
تابع شبکه (۳) را میتوان برحسب عاملهایی با بخشهای حقیقی و موهومی نوشت. در این صورت، نمایش کلی تابع شبکه بهصورت زیر است:
که صفرها و قطبهای $$ mathbf {H} (omega ) $$ را بهدست میدهد. نمایش $$ mathbf {H} (omega ) $$ در رابطه (15)، فرم استاندارد نامیده میشود. تابع $$ mathbf {H} (omega ) $$ ممکن است شامل ۷ نوع عامل مختلف باشد که به فرمهای مختلف و در ترکیبهای مختلف در تابع شبکه ظاهر میشوند. این عاملها عبارتند از:
برای بهدست آوردن نمودار بُد، عاملها را بهصورت جداگانه رسم، سپس آنها را با هم ترکیب میکنیم. در ادامه، نحوه رسم هریک از عاملهایی را که نام بردیم بیان میکنیم. این نمودارها را میتوان با تقریب بسیار خوبی رسم کرد.
اندازه و زاویه بهره $$K$$ بهترتیب $$ 20 log _{10} K $$ و $$ 0 ^ circ $$ است که هردو برای فرکانسهای مختلف، ثابت هستند. نمودارهای اندازه و فاز بهره در شکل 3 نشان داده شدهاند. اگر $$K$$ منفی باشد، انداز ه $$ 20 log _{10} |K| $$ باقی میماند، اما فاز $$ pm 180^ circ $$ خواهد شد.
برای صفر $$(j omega) $$ در مبدأ، اندازه $$20 log _{10} omega $$ و فاز $$90 ^ circ $$ است. این نمودارها در شکل ۴ رسم شدهاند. شیب نمودار اندازه، $$ 20 ,, mathrm {dB/ decade} $$ است، در حالی که مقدار فاز ثابت است.پاسخ فركانسي چيست
نمودار بُد قطب $$ (j omega )^ {-1} $$ شبیه نمودار صفر است، با این تفاوت که شیب آن $$ -20 ,, mathrm {dB/ decade} $$ و فاز $$ -90 ^ circ $$ است. در حالت کلی، برای $$ (j omega ) ^N$$ که $$N$$ یک عدد صحیح است، نمودار اندازه دارای شیب $$ 20N ,, mathrm{dB/decade} $$ است، در حالی که فاز $$ 90N $$ است.
برای صفر ساده $$(1+j omega / z_1)$$، اندازه $$ 20 ,, log _{10} |1+j omega / z_1 | $$ و فاز $$ tan ^ {-1} omega / z_1 $$ را داریم. در این حالت:
روابط اخیر نشان میدهند که میتوان برای مقادیر کوچک $$ omega $$ اندازه را با صفر (یک خط راست با شیب صفر) و برای مقادیر $$ omega $$ بزرگ با یک خط راست با شیب $$ 20 ,, mathrm {dB/ decade} $$ تقریب زد. فرکانس $$ omega = z _1 $$ که در آن، دو خط مجانب به یکدیگر میرسند، «فرکانس گوشه» (Corner Frequency) یا «فرکانس شکست» (Break Frequency) نامیده میشود. نمودار تقریبی اندازه و نمودار دقیق آن در شکل ۵ (الف) نشان داده شدهاند.
توجه کنید که نمودار تقریبی، به نمودار دقیق نزدیک است؛ جز در فرکانس شکست $$ omega = z_1$$ که مقدار اختلاف برابر است با $$20 , log _{10} |(1+j1)|=20, log _{10} sqrt {2} approx 3 , mathrm {dB}$$.
فاز $$ tan ^ {-1} ( frac{omega}{z_1}) $$ را میتوان بهصورت زیر نوشت:
در تقریب خط راست، فاز $$ phi approx 0 $$ را برای $$ omega le z_1/10 $$ و $$phi approx 45^ circ $$ را برای $$ omega = z_1$$ و $$ phi approx 90^ circ $$ را برای $$ omega ge 10 z_1 $$ در نظر میگیریم.
نمودارهای بُد برای قطب $$ 1/(1+ jomega / p_1 ) $$ مشابه شکل ۵ هستند، جز فرکانس گوشه $$ omega = p_1 $$ که شیب اندازه $$ -20 , mathrm{dB/decade}$$ و شیب فاز $$-45 ^ circ $$ بر دهه (decade) است.
اندازه قطب درجه دوم $$ 1/ [1+ j2 zeta _2 omega / omega _n + (j omega / omega _n)^2] $$ برابر با $$ -20 log _{10} | 1+ j 2 zeta _2 omega / omega _n + j omega / omega _n + (j omega / omega _n)^2| $$ و فاز آن، معادلِ $$ tan ^ {-1} ( 2 zeta _2 omega / omega _n )/ (1- omega ^2 / omega _n^2) $$ است. برای فرکانسهای کوچک داریم:
و در فرکانسهای بزرگ:
بنابراین، نمودار اندازه دو خط مجانب دارد: یکی با شیب صفر برای $$ omega omega _n $$ که $$omega _n $$ فرکانس گوشه است.
شکل ۶ (الف)، نمودارهای اندازه تقریبی و دقیق را نشان میدهد. نمودار دقیق، به ضریب میرایی $$ zeta _2 $$ و فرکانس گوشه $$ omega _n $$ بستگی دارد. اگر دقت بالایی لازم باشد، پیک قابلتوجه در مجاورت فرکانس گوشه را باید به تقریب خطی افزود.
نمودار فاز، خط راستی با شیب $$ -90 ^ circ $$ بر دهه است که از $$ omega _n $$ شروع شده و در $$ 10 omega _n $$ تمام میشود (شکل ۶ (ب)). مجدداً میبینیم که اختلاف نمودار دقیق و خط تقریبی بهدلیل ضریب میرایی است.
تقریب خطی نمودارهای اندازه و فاز برای قطبهای مرتبه دوم مشابه قطبهای تکراری $$ (1+j omega / omega _n ) ^{-2} $$ است. قطبهای تکراری، معادل قطب درجه دوم با $$ zeta _2 = 1 $$ هستند.
برای صفر درجه دوم، نمودارهای شکل ۶ معکوس میشوند، زیرا شیب نمودار اندازه $$ 40 , mathrm {dB/decade}$$ و شیب نمودار فاز $$ 90 ^ circ $$ بر دهه است.
جدول ۲، خلاصه نمودارهای بُد را برای هفت عامل نشان میدهد. البته در عمل، هر تابع شبکه همه هفت عامل را ندارد. برای رسم نمودارهای بُد تابع شبکه $$ mathbf{H} ( omega ) $$ بهفرم رابطه (۱۵)، ابتدا فرکانسهای گوشه را در نمودار نیمهلگاریتمی مشخص میکنیم، سپس نمودار عاملها را با هم ترکیب میکنیم. نمودار ترکیبی، اغلب از چپ به راست و با تغییر مناسب شیبها در هر فرکانس گوشه رسم میشود.
نمودارهای بُد تابع زیر را رسم کنید:
حل: ابتدا $$mathbf {H} (omega ) $$ را با تقسیم قطبها و صفرها بهفرم استاندارد مینویسیم:
بنابراین، اندازه و فاز بهصورت زیر هستند:
همانطور که میبینیم، دو فرکانس گوشه در $$ omega =2, 10 $$ داریم. نمودار اندازه و فاز هر جمله با خط منقطع رسم، سپس با هم ترکیب شده و خط ممتد به دست آمده است (شکل 7).
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^
سید سراج حمیدی (+)
«سید سراج حمیدی» دانشآموخته مهندسی برق است. او مدتی در زمینه انرژیهای تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزشهای ریاضیات، مهندسی برق و بورس مجله فرادرس را مینویسد.
بر اساس رای 4 نفر
آیا این مطلب برای شما مفید بود؟
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
سازمان علمی و آموزشی «فرادرس» (Faradars) از قدیمیترین وبسایتهای یادگیری آنلاین است که توانسته طی بیش از ده سال فعالیت خود بالغ بر ۱۱۰۰۰ ساعت آموزش ویدیویی در قالب فراتر از ۲۰۰۰ عنوان علمی، مهارتی و کاربردی را منتشر کند و به بزرگترین پلتفرم آموزشی ایران مبدل شود.
فرادرس با پایبندی به شعار «دانش در دسترس همه، همیشه و همه جا» با همکاری بیش از ۱۳۰۰ مدرس برجسته در زمینههای علمی گوناگون از جمله آمار و دادهکاوی، هوش مصنوعی، برنامهنویسی، طراحی و گرافیک کامپیوتری، آموزشهای دانشگاهی و تخصصی، آموزش نرمافزارهای گوناگون، دروس رسمی دبیرستان و پیش دانشگاهی، آموزشهای دانشآموزی و نوجوانان، آموزش زبانهای خارجی، مهندسی برق، الکترونیک و رباتیک، مهندسی کنترل، مهندسی مکانیک، مهندسی شیمی، مهندسی صنایع، مهندسی معماری و مهندسی عمران توانسته بستری را فراهم کند تا افراد با شرایط مختلف زمانی، مکانی و جسمانی بتوانند با بهرهگیری از آموزشهای با کیفیت، به روز و مهارتمحور همواره به یادگیری بپردازند. شما هم با پیوستن به جمع بزرگ و بالغ بر ۴۰۰ هزار نفری دانشجویان و دانشآموزان فرادرس و با بهرهگیری از آموزشهای آن، میتوانید تجربهای متفاوت از علم و مهارتآموزی داشته باشید.
مشاهده بیشتر
© فرادرس ۱۳۸۹-۱۳۹۷. تمامی حقوق محفوظ است.
گزارشهای بازدید دانشکده
پاسخ فركانسي چيست
تابع پاسخ فرکانسی
تابع پاسخ فرکانسی [1] حاصل تقسیم پاسخ سیستم بر ورودی سیستم در فضای فرکانس تعریف میشود (رابطه 1). و عموما با ماتریس H نشان داده میشود. بطور مشابه، معکوس تابع پاسخ فرکانسی، حاصل تقسیم ورودی بر پاسخ سیستم در فضای فرکانس میباشد که بطور عمومی با ماتریس Z نشان داده میشود. اگر پاسخ سیستم به ترتیب تغییرمکان، سرعت و شتاب منظور شود، تابع پاسخ فرکانسی به ترتیب نرمی دینامیکی [2] ، جنبایی [3] و لختایی [4] خوانده میشود. در این صورت معکوس تابع پاسخ فرکانسی به ترتیب سختی دینامیکی [5] ، امپدانس مکانیکی [6] و جرم آشکار [7] خواهد بود.
رابطه (1-الف)
رابطه (1-ب)
رابطه (1-ج)
صفر [8] و قطب [9] درایههای ماتریس سختی دینامیکی به ترتیب به قطب و صفر در ماتریس نرمی دینامیکی تبدیل میگردد. فرکانسهایی که ماتریس سختی صفر میشود و یا قطب ماتریس نرمی دینامیکی است، فرکانس تشدید [10] و فرکانسهایی که قطب ماتریس سختی و یا صفر ماتریس نرمی دینامیکی است، فرکانس ضد تشدید [11] خوانده میشود. درایههای اشکال مختلف تابع پاسخ فرکانسی به شکل رابطه (2) تعریف میشود. مثلا درایهی jk ا م ماتریس نرمی دینامیکی، حاصل تقسیم تغییرمکان گرهی j ا م بر نیروی وارد شده در گرهی k ام در فضای فرکانسی میباشد وقتیکه باری در سایر گرهها وارد نشود.
رابطه (2-الف)
رابطه (2-ب)
رابطه (2-ج)
شکلهای مودی و فرکانسهای ارتعاشی از تجزیه مقادیر سینگولار [12] ماتریس نرمی دینامیکی قابل محاسبه است. وقتی سیستم خود الحاق [13] با میرایی متناسب باشد، بردارهای ویژه حقیقی هستند و مقادیر ویژه بدلیل وجود میرایی مختلط هستند (رابطه 3-الف). در این حالت اگر میرایی غیرمتناسب باشد، بردارهای ویژه مختلط میشود و بصورت و در میآیند و مقادیر ویژه بجای بصورت مزدوج و میگردد. در حالت عمومی که سیستم غیرخود الحاق با ماتریسهای سیستم غیرمتقارن میباشد، سیستم بردارهای ویژه راست و چپ مختلط خواهد داشت (رابطه 3-ب)
رابطه (3-الف)
رابطه (3-ب)
واضح است که اندازهگیری معکوس تابع پاسخ فرکانسی از اندازهگیری مستقیم تابع پاسخ فرکانسی عملیتر است. چرا که برای اندازهگیری مستقیم تابع پاسخ فرکانسی، تمام درجات آزادی جز یکی باید بسته شود، که در عمل کاری ناممکن است. حال آنکه معکوس تابع پاسخ فرکانسی با اعمال نیروی تحریک واحد دریکی از درجات آزادی و اندازهگیری پاسخ در سایر درجات آزادی، قابل انجام است. همچنین باید توجه کرد با افزایش یا کاهش دقت مدلسازی و ایجاد تغییر در درجات آزادی، تابع پاسخ فرکانسی تغییر میکند، حال آنکه معکوس تابع پاسخ فرکانسی، تغییری نمینماید.
ماکزیممهای تابع پاسخ فرکانسی نرمی دینامیکی، جنبایی و لختایی، متناظر با فرکانسهای تشدید سیستم و مینیممهای آن متناظر با فرکانسهای ضد تشدید میباشد. بطور کلی، رفتار تابع قبل از فرکانس ضدتشدید تا نزدیکی فرکانس تشدید هر مود، به سختی آن مود بستگی دارد. در محدودهی رزونانس به میرایی مود بستگی پیدا میکند و از اندکی پس از فرکانس تشدید تا فرکانس ضدتشدید دیگر، به جرم متناظر با آن مود وابسته است. تابع پاسخ فرکانسی المان سختی، میرایی ویسکوز و جرم در جدول (1) نشان داده شده است.
جدول 1- تابع پاسخ فرکانسی المان سختی، میرایی ویسکوز و جرم
سختی
میرایی ویسکوز
جرم
پارامترهای تابع پاسخ فرکانسی
نرمی دینامیکی
پاسخ فركانسي چيست
جنبایی
لختایی
[1] frequency response function (FRF)
[2] receptance
[3] mobility
[4] inertance
[5] dynamic stiffness
[6] mechanical impedance
[7] apparent mass
[8] zero
[9] pole
[10] resonance frequency
[11] anti-resonance frequency
[12] singular value decomposition
[13] self adjoint
%PDF-1.6
%
295 0 obj
>stream
8]D-f՝t;^@(}s&,n+76t5’D5װN+&5LнPɫ, `pX.ސ|hpU1U2ԎT,V-Rúlz,]&Iyer”~n
/zO{;a1]dUޏ[8@(W0
تابع شبکه و پاسخ فرکانسی
در این فیلم آموزشی درباره تابع شبکه و پاسخ فرکانسی بحث می کنیم.
[۱] Hayt, William, Jack Kemmerly, and Steven Durbin. Engineering ciRLuit analysis. McGraw-Hill, 2011.
دانلود جزوه
دانلود ویدئو
پاسخ فركانسي چيست
(۱۴۶۵)
نوشته ها
برگه ها
دسته ها
برچسب ها
*نام و نام خانوادگی*آدرس ایمیل
*عنوان ویدئو
دانشگاهیدبیرستانیآموزش نرم افزارسایر
رشته
درس
*مسیر آپلود ویدئو
تصویر شاخص
جزوه ویدئو
توضیح ویدئو
تابع شبکه و پاسخ فرکانسی
در این فیلم آموزشی درباره تابع شبکه و پاسخ فرکانسی بحث می کنیم.
[۱] Hayt, William, Jack Kemmerly, and Steven Durbin. Engineering ciRLuit analysis. McGraw-Hill, 2011.
دانلود جزوه
دانلود ویدئو
پاسخ فركانسي چيست
(۱۴۶۵)
نوشته ها
برگه ها
دسته ها
برچسب ها
*نام و نام خانوادگی*آدرس ایمیل
*عنوان ویدئو
دانشگاهیدبیرستانیآموزش نرم افزارسایر
رشته
درس
*مسیر آپلود ویدئو
تصویر شاخص
جزوه ویدئو
توضیح ویدئو
با IT-Planet دنیای آیتی را بهتر بشناسید
آموزش
سیارهآیتی
آیا تاکنون با عبارت 20Hz-20KHz روی جعبهی هدفون یا اسپیکر روبرو شدهاید؟ یکی از مشخصات هدفون یا به طور کلی سیستمهای پخش صدا، قابلیت پخش صداهایی با فرکانس بسیار کم یا زیاد است. به عنوان مثال ممکن است روی جعبهی محصول یا در صفحهی مشخصات، عبارت 20Hz-20KHz درج شود که به معنی قدرت پخش صداهایی با فرکانس ۲۰ هرتز الی ۲۰ هزار هرتز است.
در این مقاله به بررسی مفهوم هرتز در سیستمهای پخش صدا مثل بلندگو، سینمای خانگی، هدفون و هدست و ایرفون یا اسپیکر میپردازیم. با ما باشید.پاسخ فركانسي چيست
در هر سیستم پخش صدا که معمولی و برای شنوایی توسط انسان طراحی شده باشد، محدودهی فرکانسهایی که قابلیت ایجاد و پخش شدن دارد، از چند ده هرتز شروع میشود و به عددی در حدود ۲۰ کیلوهرتز میرسد. به عنوان مثال ممکن است یک سیستم صوتی مرغوب بتواند صداهایی با فرکانس ۱۶ هرتز الی ۲۶ کیلوهرتز را پخش کند.
توجه کنید که ۲۰ کیلوهرتز معادل ۲۰ هزار هرتز است و کیلو مفهومی جز ۱۰۰۰ واحد ندارد. حال آنکه ممکن است در مورد وزن و توان و ولتاژ از واحد کیلوگرم و کیلووات و کیلوولت استفاده شود.
اما منظور از ۱ هرتز چیست؟
هر هرتز به معنی ۱ نوسان در ثانیه است. Hertz نام دانشمندی است که مفهوم فرکانس را مطرح کرده و از این رو برای بیان تعداد نوسان در ثانیه، از هرتز استفاده میشود.
در مورد صدا، ۱ هرتز به معنی یک بار جلو و عقب رفتن دیافراگم بلندگو است و طبعاً ۲۰ کیلوهرتز به معنی ۲۰ هزار بار جلو و عقب رفتن دیافراگم است که البته چیزی نیست که حس لامسهی انگشتان دست، آن را به راحتی تشخیص دهد.
برای اطلاعات بیشتر در مورد انواع بلندگو که صداهای بم یا زیر را پخش میکنند و به خصوص آشنایی با Woofer یا ساب، به مقالهای دیگر از بخش دانشنامهی سیارهی آیتی توجه فرمایید:
ممکن است در یک سیستم پخش صدا، برخی بلندگوها فقط صداهای بم با فرکانس ۴ الی ۱۰۰ هرتز را پخش کنند اما در صفحهی مشخصات کلی سیستم، پاسخ فرکانسی یا همان محدودهی پخش صدا، ۴ هرتز الی ۲۶ کیلوهرتز عنوان شود.
اغلب وسایل پخش موسیقی و لوازم صوتی، عملاً صداهایی در محدودهی ۸۰ هرتز الی ۱۵۰۰۰ هرتز را دریافت یا پخش میکنند. صداهایی با فرکانس کمتر یا بیشتر از این محدوده، از نظر قدرت، ضعیفتر پخش میشود و حتی در مورد برخی محصولات، برخلاف ادعای سازنده، قدرت پخش صدا عملاً در حد صفر دسیبل است!
اما آیا این ادعای کذب یک نقطه ضعف بزرگ و بسیار مهم است؟
توجه کنید که شنوایی انسان به گونهای است که صداهایی در محدودهی ۱ کیلوهرتز الی ۳ کیلوهرتز را بهتر از صداهایی بمتر یا زیرتر میشنود. به عبارت دیگر این صداها را حتی اگر قدرت کمی داشته باشند هم به خوبی میشنود اما در مورد صداهای بسیار نازک که فرکانس بیشتر از ۱۸ کیلوهرتز است، شنوایی انسان بسیار ضعیف عمل میکند و شاید اغلب افراد متوجه پخش شدن صدا نشوند! در مورد صداهای بم با فرکانس کمتر از ۱۶ هرتز هم همینطور است.
بنابراین میتوان گفت که اگر هدفون یا اسپیکری، بتواند صداهایی با فرکانس بین ۴۰ تا ۱۵ کیلوهرتز را به خوبی پخش کند، اغلب کاربران را راضی میکند. لذا تفاوت خاصی بین هدفونی که پاسخ فرکانسی یا Frequency Response آن، 16-22000Hz است با هدستی که محدودهی ۲۰ هرتز الی ۲۰ کیلوهرتز را پوشش میدهد، وجود ندارد اما معمولاً هدفونهای مرغوبتر، پاسخ فرکانسی گستردهتری دارند.
بنابراین حین خرید محصول، علاوه بر توجه به پاسخ فرکانسی، بهتر است به نقد و بررسیهای تخصصی و نظر مشتریانی که آن هدفون یا سیستم صوتی را خریداری کردهاند، توجه کنید. نمیتوان صرفاً با توجه به اعتبار یک برند، اعداد روی بستهبندی محصول یا نقد و بررسیهای یک شخص یا وبسایت خاص، تصمیمگیری کرد.
سیارهی آیتی
مهندسی مکانیک، عاشق موسیقی، انیمه و فیلم هنری، نقاشی و خطاطی و همینطور بازیهای نقشآفرینی جذاب. علاقهمند به دنیای تکنولوژی و به ویژه کامپیوتر، موبایل و تبلت.
هدفونهای وایرلس یا بیسیم انواع مختلفی دارند. برخی دارای میکروفون هستند که به آنها هدست یا هندزفری گفته میشود. برخی مبتنی بر بلوتوث طراحی شدهاند و قابلیت اتصال به محصولاتی با سیستم عامل اندروید و حتی لپتاپهای ویندوزی و غیره را دارند و برخی دیگر دارای دانگل USB خاصی برای برقراری ارتباط بیسیم هستند. ابعاد و اندازهی هدستها و هنزفریهای بلوتوثی نیز متنوع است. برخی از نوع Earbud هستند و داخل گوش پنهان میشوند و برخی دیگر روی سر قرار میگیرند و بزرگ هستند. عمر باتری این محصولات بسیار متفاوت است.
در سیستم عامل ویندوز اگر چند کارت صدا داشته باشیم، ویندوز در هر لحظه صدا را به یکی از این وسایل هدایت میکند. اما میتوان با نصب کردن برخی نرمافزارهای جانبی کاری کرد که صدای یک نرمافزار از یک خروجی پخش شود و صدای نرمافزار دیگر از یک خروجی متفاوت. به عنوان مثال صدای موسیقی از اسپیکر پخش شود و صدای فیلمی که تماشا میکنیم از هدست USB که خود دارای کارت صدای مجزا است.
یک روش سادهی تست کردن میکروفون، خرابی میکروفون و بررسی بلندی صدای میکروفون در ویندوز ۱۰ این است که صدای میکروفون را از طریق اسپیکر یا هدفون بشنوید. شنیدن صدایی که میکروفون دریافت میکند از طریق اسپیکر، کاربردهای دیگری نیز دارد. به عنوان مثال در مراسم و جشنها میتوانید برای اجرای زندهی موسیقی و خوانندگی از این روش استفاده کنید.
یکی از انواع میکروفونهای حرفهای، میکروفون XLR است. این نوع میکروفون در استدیوها و ایستگاههای رادیو و همینطور اجرای زنده به کار میرود و کابل خاصی دارد که برای انتقال بهتر سیگنال صدا و ایزوله کردن و جلوگیری از اضافه شدن نویزها، عالی است. برای استفاده از این میکروفونها، علاوه بر خود میکروفون، به میکسر یا مبدل خاصی نیاز است که توان مورد نیاز را تأمین کند و تبدیل لازم را انجام دهد.
برای نوشتن کد از
CODE
استفاده کنید.به عبارت دیگر قبل و بعد از کد
و
تایپ کنید.
نشانی ایمیل شما منتشر نخواهد شد. بخشهای موردنیاز علامتگذاری شدهاند *
document.getElementById(“comment”).setAttribute( “id”, “af3e7fe8eba372700d1aa3bcd22f2de0” );document.getElementById(“ac8fea9f75”).setAttribute( “id”, “comment” );
نام:
ایمیل:
برای دنبال کردن نظرات و پاسخها، پایین صفحات سایت یا صفحهی ۲۰۰ دیدگاه آخر را دنبال بفرمایید.
بازنشر مطالب در رسانهها تنها با ذکر نویسنده و نام منبع:
it-planet.irمجاز است.
پاسخ فرکانسی به رِنجی از صداهای زیر، میانه و بالا میگویند، که درایور یک هدفون توانائی باز تولید آنرا از پائینترین تا بالاترین تُن صدائی دارا باشد. بسیاری از علاقهمندان موسیقی، از ما هدفونهائی با صدای بسیار صاف و تائید شده طلب میکنند. چیزی که آنها توصیف میکنند یک صدای بالانس شده است، که فرکانسهای آن بصورت برابر در تمامی رنجهای فرکانس هدفون توزیع شده باشد. بسیاری از علاقهمندان موسیقی ایرانی به هدفونهائی با بالانس میانه نیاز دارند.
میانگین دایرهی فرکانس شنوائی انسان بین ۲۰ هرتز تا ۲۰ هزار هرتز است. در حالی که فرکانس هدفون های معمولی، عددی میان همین رنج را پوشش می دهند؛ هدفونهائی با فرکانس پائین ( حتی تا ۵ هرتز ) و همچنین هدفونهائی با فرکانس بالا ( تا ۳۵ هزار هرتز ) هم وجود دارد. شاید بپرسید چگونه یک انسان توانائی شنیدن این رنج صدا را دارد؟ پاسخ این است : شاید این فرکانسها هرگز شنیده نشوند، اما قطعا احساس خواهند شد؛ و این موضوع مطمئنا، به ارتقای سطح تجربهی شنوائی شما از یک هدفون منجر میشود.
در فرکانس پائین شما بیشتر صداهای ضربهای و بم را میشنوید و در نقطه ی مقابل، در فرکانسهای بالا صدای تیز و تند، بیشتر به گوش میرسد. روش علمی و صحیح انتخاب یک هدفون میبایست بر پایهی نیازهای موسیقائی ژانر انتخابی شما باشد. برای سبکهای شرقی، EDM ( Electronic Dance Music )، پاپ، Ragge ( نوعی موسیقی پر بیت جامائیکائی )، تکنو و سبکهای دیسکوئی، فرکانس هدفون پائین مناسبتر هستند. هدفونهای فرکانس بالا اما شما را قادر خواهند کرد تا تمامی و هر بیت یک موسیقی اصیل هِوی متال ( Heavy Metal ) را بشنوید. افرادی هم که به سبک بزرگان موسیقی کلاسیک، مانند موتزارت و باخ علاقهمند هستند، به هدفونهائی بدون هیچگونه تمایل فرکانسی نیاز خواهند داشت.
✓ شاید نیاز به خرید هدفون داشته باشید؛ از بخش انواع هندزفری ، هدفون و هدست وبسایت ما دیدن فرمایید..پاسخ فركانسي چيست
.
.
در حالی که گستردگی دامنهی فرکانس هدفون، لزوما به معنای کیفیت بالای آن نیز به حساب نمیآید؛ اما باید بدانید بسیاری از جزئیات موسیقائی در آنها شنیده میشود. یک آهنگ به گونهای نوشته و تنظیم میگردد، که با استفاده از تمامی آلات موسیقی ممکن، تمامی بخشهای خود را تکمیل کند. این صداها در طیف گستردهای از تنهای صدائی پراکنده میگردد، و شما تنها در صورتی قادر به شنیدن آنها هستید که، هدفون شما این قابلیت را داشته باشد؛ البته اگر انتخاب درستی کرده باشید.
.
.
اندازهگیری میزان پاسخ فرکانسی یک هدفون کار آسانی نیست. نحوهی اندازهگیری آن به این صورت است: باید به کمک یک میکروفن فوق حساس در تمامی فرکانسها، باز تولید صدا را از هدفون ضبط کنید. میکروفن دقیقا باید در مرکز هدفون قرار بگیرد. حالا شما میتوانید، واکنش هدفون به هر صدائی را به درستی اندازهگیری کرده و بر روی نمودار بیاورید.
” تقریبا ۲۰ سال است که، در تلاش مستمر برای اندازه گیری درست صدای انواع هدفون هستم. برای این موضوع بسیار زمان گذاشته و فکر کردهام؛ و پاسخ همیشه در نظرم بسیار واضح و مشخص بوده است. ”
نشانی ایمیل شما منتشر نخواهد شد.
دیدگاه
نام
ایمیل
وب سایت
نام و نام خانوادگی (الزامی)
شماره تماس (الزامی)
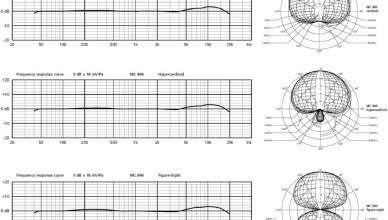
دیدگاهتان را بنویسید